Co-ordinate Geometry - Solved Examples

Advertisements

Previous Page
Next Page  

Q 1 - In which quadrant does the given point (-2, 3) lies?

A - II

B - III

C - IV

D - I

Answer - A

Explanation

Plane
(-2, 3) lies in quadrant II.

Q 2 - Find the distance between the points A (-4, 7) and B (2, 5).

A - 5

B - 6

C - 6√5

D - 7

Answer - C

Explanation

AB = √(2+4)2 + (-5-7)2 = √62+ (-12)2 = √36+144 = √180
=√36*5 = 6√5 units.

Q 3 - Find the distance of the point A (6,-6) from the origin.

A - 5

B - 6

C - 6√5

D - 6√2

Answer - D

Explanation

OA = √62+ (-6)2 =√36+36 =√72 = √36*2 = 6√2 units.

Q 4 - Show that the points A(0,-2) ,B(3,1) ,C(0,4) and D(-3,1) are the vertices of a square.

A - false

B - true

Answer - B

Explanation

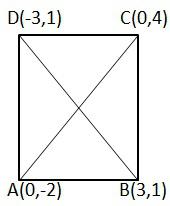square
AB2= (3-0)2+ (1+2)2= (9+9) =18	
BC2= (0-3)2+ (4-1)2= (9+9) =18
CD2= (0-3)2+ (1+2)2= (9+9) =18 
DA2= (-3-0)2+ (1+2)2= (9+9) =18   
∴ AB= BC=CD=DA = √18 = √9*2 = 3√2
AC2=(0-0)2+(4+2)2= (0+36) =36
BD2= (-3-3)2+ (1-1)2= (36+0) =36
∴ Diag AC = Diag BD = 6
Thus all sides are equal and the diagonals are equal.
∴ ABCD is a square.

Q 5 - Show that the points P(-4,-1), Q(-2,-4),R(4,0) and S(2,3) are the vertices of a rectangle.

A - false

B - true

Answer - B

Explanation

rectangle
PQ2= (-2+4)2+ (-4+1)2= 22+ (-3)2= (4+9) =13
QR2= (4+2)2+ (0+4)2= (62+42) = (36+16) =52
RS2= (2-4)2= (3-0)2= (-2)2+32= (4+9) = 13
SP2= (2+4)2+ (3+1)2= (62+42) = (36+16) = 52
∴ PQ=RS =√13 AND QR=SP =√52
PR2= (4+4)2+ (0+1)2= (82+12) = (64+1) =65
QS2= (2+2)2+ (3+4)2= (42+72) = (16+49) =65
∴ Diag PR= Diag QS =√ 65 
Thus, opposite sides are equal and diagonals are equal.
∴ ABCD is a rectangle.

Q 6 - Show that the points A (-3, 2), B (-5-5), C (2-3) and D (4, 4) are the vertices of a rhombus.

A - false

B - true

Answer - B

Explanation

rhombus
AB2= (-5+3)2+ (-5-2)2= (-2)2+ (-7)2= (4+49) =53
BC2= (2+5)2+ (-3+5)2= (7)2+ (2)2= (49+4) =53
CD2= (4-2)2+ (4+3)2= (22+72) = (4+49) =53
DA2= (4+3)2+ (4-2)2= (72+22) = (49+4) =53
∴ AB=BC=CD=DA = √53                               
AC2= (2+3)2+ (-3-2)2= (52) + (-5)2= (25+25) = 50
BD2= (4+5)2+ (4+5)2= (92) + (92) = (81+81) =162
∴ Diag AC ≠ Diag BD
Thus all the sides are equal and diagonals are not equal.
∴ ABCD is a Rhombus.

Q 7 - Discover the region of ABC whose vertices are A (10, - 6), B (2, 5) and C (- 1, 3).

A - 49/2 sq.units.

B - 47/2 sq.units.

C - 45/2 sq.units.

D - 43/2 sq.units.

Answer - A

Explanation

Here x1=10, x2=2, X3 = -1 and y1= - 6, y2= 5, y3= 3 
∴ ∆= 1/2 {X1(y2-Y3) +x2(Y3-Y1) +X3 (Y1-Y2)} 
=1/2 {10(5-3) +2(3+6) - 1(- 6-5) = 1/2 (20+18+11) =49/2 sq.units.

Q 8 - Discover the estimation of h for which the focuses A (- 1, 3), B (2, h) and C (5, - 1) are collinear.

A - 1

B - 2

C - 3

D - 4

Answer - A

Explanation

Here x1=-1, x2=2, x3=5 and y1=3, y2=h and Y3=-1 
Now, ∆=0 ⇒ X1(y2-Y3) +x2(Y3-Y1) +X3(Y1-Y2) = 0
⇒ -1(h+1) +2(-1-3) +5(3-h) =0
⇒ -h-1-8+15-5h=0 ⇒ 6h=6 ⇒ h=1

Q 9 - Discover the co-ordinates of the centroid of ∆ABC whose vertices are A (6, - 2) and B (4, - 3) what's more, C (- 1, - 4).

A - (-3,-3)

B - (3,3)

C - (3,-3)

D - (-3,3)

Answer - C

Explanation

The directions of the centroid are 
{(6+4-1)/3, (- 2-3-4)/3} i.e. (3, - 3)

Q 10 - Discover the proportion in which the point p (2, - 5) partitions the line portion AB joining A (- 3, 5) what’s more, B (4, - 9).

A - 1:2

B - 5:2

C - 2:5

D - 2:1

Answer - B

Explanation

Let the required proportion be x:1. 
At that point (4x-3/x+1, - 9 x+5/x+1) concurs with p (2, - 5) 
∴ 4x-3/ ( x+1) =2 ⇒ 4x-3 = 2x+2 ⇒ 2x=5 ⇒ x=5/2 
∴ required proportion is 5/2:1 i.e. 5:2

Q 11 - . Discover the slop of the line whose slant is 30°?

A - 1/√3

B - 2/√3

C - 3/√3

D - 4/√3

Answer - A

Explanation

m= tan 30° = 1/√3

Q 12 -Discover the slant of line whose slop is 1/√3

A - 30°

B - 60°

C - 80°

D - Cannot be computed with the given information

Answer - A

Explanation

tan x = 1/√3 ⇒ x=30°

Q 13 - Discover the slop of the line which goes through focuses A (- 2, 3) and B (4, - 6).

A - 3/2

B - -3/2

C - 3/4

D - 3/5

Answer - B

Explanation

Slop of AB = y2-y1/x2-x1 = - 6-3/4+2 = - 9/6 = - 3/2

Q 14 - Discover the slop of the line whose mathematical statement is 3x+4y-5 = 0.

A - 3/4

B - -3/4

C - 1/4

D - -1/4

Answer - B

Explanation

3x+4y-5 = 0 ∴ 4y=-3x+5 ∴ y=-3/4x+5/4 
∴ slop = m =-3/4

Q 15 - Discover the estimation of h for which the line 2x+3y-4 = 0 and hx+6y+5 =0 are parallel.

A - 2

B - 3

C - 4

D - 5

Answer - C

Explanation

2x+3y - 4 =0 ⇒ 3y= - 2x+4 ⇒y= - 2x/3 +4/3 
hx+6y+5 =0 ⇒ 6y =-hx-5 ⇒ y= - hx/6 - 5/6 
The line will be parallel if - h/6 -2/3 ⇒ h= (2/3*6) = 4
∴ h=4

Q 16 - Discover the estimation of h for which the lines 5x+3y +2=0 and 3x-hy+6= 0are perpendicular to each other.

A - 2

B - 3

C - 4

D - 5

Answer - D

Explanation

5x+3y+2 =0 = -5x-2 ⇒ y= -5x/3-2/3
3x- hy+6 =0 ⇒ hy =   3x+6 ⇒ y =3x/h+6/h
The line will be perpendicular to each other if -5/3* 3/h= -1 ⇒ h=5.
Hence h= 5.
aptitude_coordinate_geometry.htm
Advertisements