DSP - Miscellaneous Signals

There are other signals, which are a result of operation performed on them. Some common type of signals are discussed below.

Conjugate Signals

Signals, which satisfies the condition $x(t) = x*(-t)$ are called conjugate signals.

Let $x(t) = a(t)+jb(t)$...eqn. 1

So, $x(-t) = a(-t)+jb(-t)$

And $x*(-t) = a(-t)-jb(-t)$...eqn. 2

By Condition, $x(t) = x*(-t)$

If we compare both the derived equations 1 and 2, we can see that the real part is even, whereas the imaginary part is odd. This is the condition for a signal to be a conjugate type.

Conjugate Anti-Symmetric Signals

Signals, which satisfy the condition $x(t) = -x*(-t)$ are called conjugate anti-symmetric signal

Let $x(t) = a(t)+jb(t)$...eqn. 1

So $x(-t) = a(-t)+jb(-t)$

And $x*(-t) = a(-t)-jb(-t)$

$-x*(-t) = -a(-t)+jb(-t)$...eqn. 2

By Condition $x(t) = -x*(-t)$

Now, again compare, both the equations just as we did for conjugate signals. Here, we will find that the real part is odd and the imaginary part is even. This is the condition for a signal to become conjugate anti-symmetric type.

Example

Let the signal given be $x(t) = \sin t+jt^{2}$.

Here, the real part being $\sin t$ is odd and the imaginary part being $t^2$ is even. So, this signal can be classified as conjugate anti-symmetric signal.

Any function can be divided into two parts. One part being Conjugate symmetry and other part being conjugate anti-symmetric. So any signal x(t) can be written as

Where $xcs(t)$ is conjugate symmetric signal and $xcas(t)$ is conjugate anti symmetric signal

And

Half Wave Symmetric Signals

When a signal satisfies the condition $cx(t) = -x(t\pm (\frac{T_{0}}{2}))$, it is called half wave symmetric signal. Here, amplitude reversal and time shifting of the signal takes place by half time. For half wave symmetric signal, average value will be zero but this is not the case when the situation is reversed.

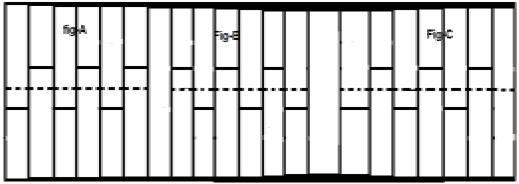
Consider a signal x(t) as shown in figure A above. The first step is to time shift the signal and make it $x[t-(\frac{T}{2})]$. So, the new signal is changed as shown in figure B. Next, we reverse the amplitude of the signal, i.e. make it $-x[t-(\frac{T}{2})]$ as shown in figure C. Since, this signal repeats itself after half-time shifting and reversal of amplitude, it is a half wave symmetric signal.

Orthogonal Signal

Two signals x(t) and y(t) are said to be orthogonal if they satisfy the following two conditions.

Condition 1 − $\int_{-\infty}^{\infty}x(t)y(t) = 0$ [for non-periodic signal]

Condition 2 − $\int x(t)y(t) = 0$ [For periodic Signal]

The signals, which contain odd harmonics (3^rd, 5^th, 7^th ...etc.) and have different frequencies, are mutually orthogonal to each other.

In trigonometric type signals, sine functions and cosine functions are also orthogonal to each other; provided, they have same frequency and are in same phase. In the same manner DC (Direct current signals) and sinusoidal signals are also orthogonal to each other. If x(t) and y(t) are two orthogonal signals and $z(t) = x(t)+y(t)$ then the power and energy of z(t) can be written as ;

Example

Analyze the signal: $z(t) = 3+4\sin(2\pi t+30^0)$

Here, the signal comprises of a DC signal (3) and one sine function. So, by property this signal is an orthogonal signal and the two sub-signals in it are mutually orthogonal to each other.