Principles of Satellite Communications
A satellite is a body that moves around another body in a mathematically predictable path called an Orbit. A communication satellite is nothing but a microwave repeater station in space that is helpful in telecommunications, radio, and television along with internet applications.
A repeater is a circuit which increases the strength of the signal it receives and retransmits it. But here this repeater works as a transponder, which changes the frequency band of the transmitted signal, from the received one.
The frequency with which the signal is sent into the space is called Uplink frequency, while the frequency with which it is sent by the transponder is Downlink frequency.
The following figure illustrates this concept clearly.

Now, let us have a look at the advantages, disadvantages and applications of satellite communications.
Satellite Communication − Advantages
There are many Advantages of satellite communications such as −
Flexibility
Ease in installing new circuits
Distances are easily covered and cost doesn’t matter
Broadcasting possibilities
Each and every corner of earth is covered
User can control the network
Satellite Communication − Disadvantages
Satellite communication has the following drawbacks −
The initial costs such as segment and launch costs are too high.
Congestion of frequencies
Interference and propagation
Satellite Communication − Applications
Satellite communication finds its applications in the following areas −
In Radio broadcasting.
In TV broadcasting such as DTH.
In Internet applications such as providing Internet connection for data transfer, GPS applications, Internet surfing, etc.
For voice communications.
For research and development sector, in many areas.
In military applications and navigations.
The orientation of the satellite in its orbit depends upon the three laws called as Kepler’s laws.
Kepler’s Laws
Johannes Kepler (1571-1630) the astronomical scientist, gave 3 revolutionary laws, regarding the motion of satellites. The path followed by a satellite around its primary (the earth) is an ellipse. Ellipse has two foci - F1 and F2, the earth being one of them.
If the distance from the center of the object to a point on its elliptical path is considered, then the farthest point of an ellipse from the center is called as apogee and the shortest point of an ellipse from the center is called as perigee.
Kepler’s 1st Law
Kepler’s 1st law states that, “every planet revolves around the sun in an elliptical orbit, with sun as one of its foci.” As such, a satellite moves in an elliptical path with earth as one of its foci.
The semi major axis of the ellipse is denoted as ‘a’ and semi minor axis is denoted as b. Therefore, the eccentricity e of this system can be written as −
$$e = \frac{\sqrt{a^{2}-b^{2}}}{a}$$
Eccentricity (e) − It is the parameter which defines the difference in the shape of the ellipse rather than that of a circle.
Semi-major axis (a) − It is the longest diameter drawn joining the two foci along the center, which touches both the apogees (farthest points of an ellipse from the center).
Semi-minor axis (b) − It is the shortest diameter drawn through the center which touches both the perigees (shortest points of an ellipse from the center).
These are well described in the following figure.
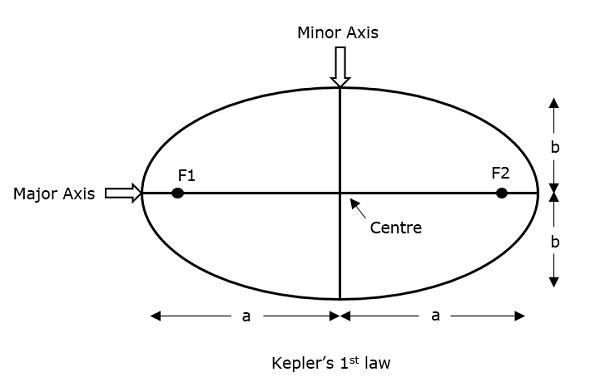
For an elliptical path, it is always desirable that the eccentricity should lie in between 0 and 1, i.e. 0 < e < 1 because if e becomes zero, the path will be no more in elliptical shape rather it will be converted into a circular path.
Kepler’s 2nd Law
Kepler’s 2nd law states that, “For equal intervals of time, the area covered by the satellite is equal with respect to the center of the earth.”
It can be understood by taking a look at the following figure.
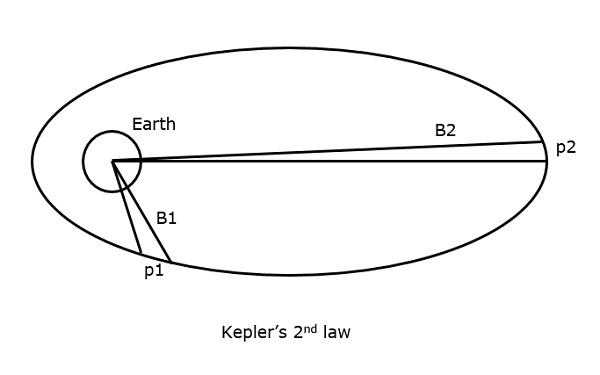
Suppose that the satellite covers p1 and p2 distances, in the same time interval, then the areas B1 and B2 covered in both instances respectively, are equal.
Kepler’s 3rd Law
Kepler’s 3rd law states that, “The square of the periodic time of the orbit is proportional to the cube of the mean distance between the two bodies.”
This can be written mathematically as
$$T^{2}\:\alpha\:\:a^{3}$$
Which implies
$$T^{2} = \frac{4\pi ^{2}}{GM}a^{3}$$
Where $\frac{4\pi ^{2}}{GM}$ is the proportionality constant (according to Newtonian Mechanics)
$$T^{2} = \frac{4\pi ^{2}}{\mu}a^{3} $$
Where μ = the earth’s geocentric gravitational constant, i.e. Μ = 3.986005 × 1014 m3/sec2
$$1 = \left ( \frac{2\pi}{T} \right )^{2}\frac{a^{3}}{\mu}$$
$$1 = n^{2}\frac{a^{3}}{\mu}\:\:\:\Rightarrow \:\:\:a^{3} = \frac{\mu}{n^{2}}$$
Where n = the mean motion of the satellite in radians per second
The orbital functioning of satellites is calculated with the help of these Kepler’s laws.
Along with these, there is an important thing which has to be noted. A satellite, when it revolves around the earth, undergoes a pulling force from the earth which is the gravitational force. Also, it experiences some pulling force from the sun and the moon. Hence, there are two forces acting on it. They are −
Centripetal force − The force that tends to draw an object moving in a trajectory path, towards itself is called as centripetal force.
Centrifugal force − The force that tends to push an object moving in a trajectory path, away from its position is called as centrifugal force.
So, a satellite has to balance these two forces to keep itself in its orbit.
Earth Orbits
A satellite when launched into space, needs to be placed in a certain orbit to provide a particular way for its revolution, so as to maintain accessibility and serve its purpose whether scientific, military, or commercial. Such orbits which are assigned to satellites, with respect to earth are called as Earth Orbits. The satellites in these orbits are Earth Orbit Satellites.
The important kinds of Earth Orbits are −
Geosynchronous Earth Orbit Satellites
A Geo-Synchronous Earth Orbit (GEO) satellite is one which is placed at an altitude of 22,300 miles above the Earth. This orbit is synchronized with a side real day (i.e., 23hours 56minutes). This orbit can have inclination and eccentricity. It may not be circular. This orbit can be tilted at the poles of the earth. But it appears stationary when observed from the Earth.
The same geo-synchronous orbit, if it is circular and in the plane of equator, it is called as geo-stationary orbit. These satellites are placed at 35,900kms (same as geosynchronous) above the Earth’s Equator and they keep on rotating with respect to earth’s direction (west to east). These satellites are considered stationary with respect to earth and hence the name implies.
Geo-Stationary Earth Orbit Satellites are used for weather forecasting, satellite TV, satellite radio and other types of global communications.
The following figure shows the difference between Geo-synchronous and Geo-stationary orbits. The axis of rotation indicates the movement of Earth.

Note − Every geo-stationary orbit is a geo-synchronous orbit. But every geo-synchronous orbit is NOT a Geo-stationary orbit.
Medium Earth Orbit Satellites
Medium Earth Orbit (MEO) satellite networks will orbit at distances of about 8000 miles from the earth's surface. Signals transmitted from a MEO satellite travel a shorter distance. This translates to improved signal strength at the receiving end. This shows that smaller, more lightweight receiving terminals can be used at the receiving end.
Since the signal is travelling a shorter distance to and from the satellite, there is less transmission delay. Transmission delay can be defined as the time it takes for a signal to travel up to a satellite and back down to a receiving station.
For real-time communications, the shorter the transmission delay, the better will be the communication system. As an example, if a GEO satellite requires 0.25 seconds for a round trip, then MEO satellite requires less than 0.1 seconds to complete the same trip. MEOs operates in the frequency range of 2 GHz and above.
Low Earth Orbit Satellites
The Low Earth Orbit (LEO) satellites are mainly classified into three categories namely, little LEOs, big LEOs, and Mega-LEOs. LEOs will orbit at a distance of 500 to 1000 miles above the earth's surface.
This relatively short distance reduces transmission delay to only 0.05 seconds. This further reduces the need for sensitive and bulky receiving equipment. Little LEOs will operate in the 800 MHz (0.8 GHz) range. Big LEOs will operate in the 2 GHz or above range, and Mega-LEOs operates in the 20-30 GHz range.
The higher frequencies associated with Mega-LEOs translates into more information carrying capacity and yields to the capability of real-time, low delay video transmission scheme.
The following figure depicts the paths of LEO, MEO, and GEO.








