Fuzzy Logic - Membership Function

We already know that fuzzy logic is not logic that is fuzzy but logic that is used to describe fuzziness. This fuzziness is best characterized by its membership function. In other words, we can say that membership function represents the degree of truth in fuzzy logic.

Following are a few important points relating to the membership function −

• Membership functions were first introduced in 1965 by Lofti A. Zadeh in his first research paper “fuzzy sets”.

• Membership functions characterize fuzziness (i.e., all the information in fuzzy set), whether the elements in fuzzy sets are discrete or continuous.

• Membership functions can be defined as a technique to solve practical problems by experience rather than knowledge.

• Membership functions are represented by graphical forms.

• Rules for defining fuzziness are fuzzy too.

Mathematical Notation

We have already studied that a fuzzy set à in the universe of information U can be defined as a set of ordered pairs and it can be represented mathematically as −

$$\widetilde{A} = \left \{ \left ( y,\mu _{\widetilde{A}} \left ( y \right ) \right ) | y\in U\right \}$$

Here $\mu \widetilde{A}\left (\bullet \right )$ = membership function of $\widetilde{A}$; this assumes values in the range from 0 to 1, i.e., $\mu \widetilde{A}\left (\bullet \right )\in \left [ 0,1 \right ]$. The membership function $\mu \widetilde{A}\left (\bullet \right )$ maps $U$ to the membership space$M$.

The dot $\left (\bullet \right )$ in the membership function described above, represents the element in a fuzzy set; whether it is discrete or continuous.

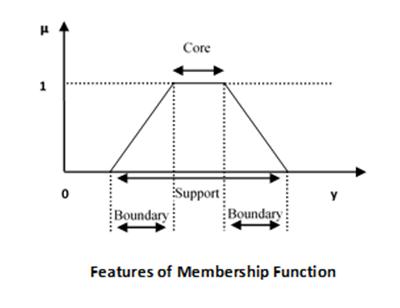
Features of Membership Functions

We will now discuss the different features of Membership Functions.

Core

For any fuzzy set $\widetilde{A}$, the core of a membership function is that region of universe that is characterize by full membership in the set. Hence, core consists of all those elements $y$ of the universe of information such that,

$$\mu _{\widetilde{A}}\left ( y \right ) = 1$$

Support

For any fuzzy set $\widetilde{A}$, the support of a membership function is the region of universe that is characterize by a nonzero membership in the set. Hence core consists of all those elements $y$ of the universe of information such that,

$$\mu _{\widetilde{A}}\left ( y \right ) > 0$$

Boundary

For any fuzzy set $\widetilde{A}$, the boundary of a membership function is the region of universe that is characterized by a nonzero but incomplete membership in the set. Hence, core consists of all those elements $y$ of the universe of information such that,

$$1 > \mu _{\widetilde{A}}\left ( y \right ) > 0$$

Fuzzification

It may be defined as the process of transforming a crisp set to a fuzzy set or a fuzzy set to fuzzier set. Basically, this operation translates accurate crisp input values into linguistic variables.

Following are the two important methods of fuzzification −

Support Fuzzification(s-fuzzification) Method

In this method, the fuzzified set can be expressed with the help of the following relation −

$$\widetilde{A} = \mu _1Q\left ( x_1 \right )+\mu _2Q\left ( x_2 \right )+...+\mu _nQ\left ( x_n \right )$$

Here the fuzzy set $Q\left ( x_i \right )$ is called as kernel of fuzzification. This method is implemented by keeping $\mu _i$ constant and $x_i$ being transformed to a fuzzy set $Q\left ( x_i \right )$.

Grade Fuzzification (g-fuzzification) Method

It is quite similar to the above method but the main difference is that it kept $x_i$ constant and $\mu _i$ is expressed as a fuzzy set.

Defuzzification

It may be defined as the process of reducing a fuzzy set into a crisp set or to convert a fuzzy member into a crisp member.

We have already studied that the fuzzification process involves conversion from crisp quantities to fuzzy quantities. In a number of engineering applications, it is necessary to defuzzify the result or rather “fuzzy result” so that it must be converted to crisp result. Mathematically, the process of Defuzzification is also called “rounding it off”.

The different methods of Defuzzification are described below −

Max-Membership Method

This method is limited to peak output functions and also known as height method. Mathematically it can be represented as follows −

$$\mu _{\widetilde{A}}\left ( x^* \right )>\mu _{\widetilde{A}}\left ( x \right ) \: for \:all\:x \in X$$

Here, $x^*$ is the defuzzified output.

Centroid Method

This method is also known as the center of area or the center of gravity method. Mathematically, the defuzzified output $x^*$ will be represented as −

$$x^* = \frac{\int \mu _{\widetilde{A}}\left ( x \right ).xdx}{\int \mu _{\widetilde{A}}\left ( x \right ).dx}$$

Weighted Average Method

In this method, each membership function is weighted by its maximum membership value. Mathematically, the defuzzified output $x^*$ will be represented as −

$$x^* = \frac{\sum \mu _{\widetilde{A}}\left ( \overline{x_i} \right ).\overline{x_i}}{\sum \mu _{\widetilde{A}}\left ( \overline{x_i} \right )}$$

Mean-Max Membership

This method is also known as the middle of the maxima. Mathematically, the defuzzified output $x^*$ will be represented as −

$$x^* = \frac{\displaystyle \sum_{i=1}^{n}\overline{x_i}}{n}$$