Fuzzy Logic - Classical Set Theory

Example

A set of all positive integers.
A set of all the planets in the solar system.
A set of all the states in India.
A set of all the lowercase letters of the alphabet.

Mathematical Representation of a Set

Sets can be represented in two ways −

Roster or Tabular Form

In this form, a set is represented by listing all the elements comprising it. The elements are enclosed within braces and separated by commas.

Following are the examples of set in Roster or Tabular Form −

Set of vowels in English alphabet, A = {a,e,i,o,u}
Set of odd numbers less than 10, B = {1,3,5,7,9}

Set Builder Notation

In this form, the set is defined by specifying a property that elements of the set have in common. The set is described as A = {x:p(x)}

Example 1 − The set {a,e,i,o,u} is written as

A = {x:x is a vowel in English alphabet}

Example 2 − The set {1,3,5,7,9} is written as

B = {x:1 ≤ x < 10 and (x%2) ≠ 0}

If an element x is a member of any set S, it is denoted by x∈S and if an element y is not a member of set S, it is denoted by y∉S.

Example − If S = {1,1.2,1.7,2},1 ∈ S but 1.5 ∉ S

Cardinality of a Set

Cardinality of a set S, denoted by |S||S|, is the number of elements of the set. The number is also referred as the cardinal number. If a set has an infinite number of elements, its cardinality is ∞∞.

Example − |{1,4,3,5}| = 4,|{1,2,3,4,5,…}| = ∞

If there are two sets X and Y, |X| = |Y| denotes two sets X and Y having same cardinality. It occurs when the number of elements in X is exactly equal to the number of elements in Y. In this case, there exists a bijective function ‘f’ from X to Y.

|X| ≤ |Y| denotes that set X’s cardinality is less than or equal to set Y’s cardinality. It occurs when the number of elements in X is less than or equal to that of Y. Here, there exists an injective function ‘f’ from X to Y.

|X| < |Y| denotes that set X’s cardinality is less than set Y’s cardinality. It occurs when the number of elements in X is less than that of Y. Here, the function ‘f’ from X to Y is injective function but not bijective.

If |X| ≤ |Y| and |X| ≤ |Y| then |X| = |Y|. The sets X and Y are commonly referred as equivalent sets.

Types of Sets

Sets can be classified into many types; some of which are finite, infinite, subset, universal, proper, singleton set, etc.

Finite Set

A set which contains a definite number of elements is called a finite set.

Example − S = {x|x ∈ N and 70 > x > 50}

Infinite Set

A set which contains infinite number of elements is called an infinite set.

Example − S = {x|x ∈ N and x > 10}

Subset

A set X is a subset of set Y (Written as X ⊆ Y) if every element of X is an element of set Y.

Example 1 − Let, X = {1,2,3,4,5,6} and Y = {1,2}. Here set Y is a subset of set X as all the elements of set Y is in set X. Hence, we can write Y⊆X.

Example 2 − Let, X = {1,2,3} and Y = {1,2,3}. Here set Y is a subset (not a proper subset) of set X as all the elements of set Y is in set X. Hence, we can write Y⊆X.

Proper Subset

The term “proper subset” can be defined as “subset of but not equal to”. A Set X is a proper subset of set Y (Written as X ⊂ Y) if every element of X is an element of set Y and |X| < |Y|.

Example − Let, X = {1,2,3,4,5,6} and Y = {1,2}. Here set Y ⊂ X, since all elements in Y are contained in X too and X has at least one element which is more than set Y.

Universal Set

It is a collection of all elements in a particular context or application. All the sets in that context or application are essentially subsets of this universal set. Universal sets are represented as U.

Example − We may define U as the set of all animals on earth. In this case, a set of all mammals is a subset of U, a set of all fishes is a subset of U, a set of all insects is a subset of U, and so on.

Empty Set or Null Set

An empty set contains no elements. It is denoted by Φ. As the number of elements in an empty set is finite, empty set is a finite set. The cardinality of empty set or null set is zero.

Example – S = {x|x ∈ N and 7 < x < 8} = Φ

Singleton Set or Unit Set

A Singleton set or Unit set contains only one element. A singleton set is denoted by {s}.

Example − S = {x|x ∈ N, 7 < x < 9} = {8}

Equal Set

If two sets contain the same elements, they are said to be equal.

Example − If A = {1,2,6} and B = {6,1,2}, they are equal as every element of set A is an element of set B and every element of set B is an element of set A.

Equivalent Set

If the cardinalities of two sets are same, they are called equivalent sets.

Example − If A = {1,2,6} and B = {16,17,22}, they are equivalent as cardinality of A is equal to the cardinality of B. i.e. |A| = |B| = 3

Overlapping Set

Two sets that have at least one common element are called overlapping sets. In case of overlapping sets −

$$n\left ( A\cup B \right ) = n\left ( A \right ) + n\left ( B \right ) - n\left ( A\cap B \right )$$

$$n\left ( A\cup B \right ) = n\left ( A-B \right )+n\left ( B-A \right )+n\left ( A\cap B \right )$$

$$n\left ( A \right ) = n\left ( A-B \right )+n\left ( A\cap B \right )$$

$$n\left ( B \right ) = n\left ( B-A \right )+n\left ( A\cap B \right )$$

Example − Let, A = {1,2,6} and B = {6,12,42}. There is a common element ‘6’, hence these sets are overlapping sets.

Disjoint Set

Two sets A and B are called disjoint sets if they do not have even one element in common. Therefore, disjoint sets have the following properties −

$$n\left ( A\cap B \right ) = \phi$$

$$n\left ( A\cup B \right ) = n\left ( A \right )+n\left ( B \right )$$

Example − Let, A = {1,2,6} and B = {7,9,14}, there is not a single common element, hence these sets are overlapping sets.

Operations on Classical Sets

Set Operations include Set Union, Set Intersection, Set Difference, Complement of Set, and Cartesian Product.

Union

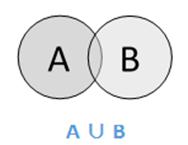
The union of sets A and B (denoted by A ∪ BA ∪ B) is the set of elements which are in A, in B, or in both A and B. Hence, A ∪ B = {x|x ∈ A OR x ∈ B}.

Example − If A = {10,11,12,13} and B = {13,14,15}, then A ∪ B = {10,11,12,13,14,15} – The common element occurs only once.

Intersection

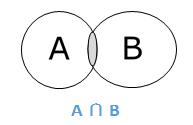
The intersection of sets A and B (denoted by A ∩ B) is the set of elements which are in both A and B. Hence, A ∩ B = {x|x ∈ A AND x ∈ B}.

Difference/ Relative Complement

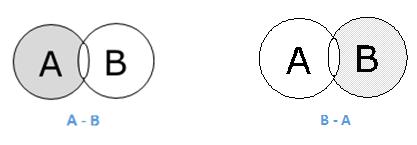
The set difference of sets A and B (denoted by A–B) is the set of elements which are only in A but not in B. Hence, A − B = {x|x ∈ A AND x ∉ B}.

Example − If A = {10,11,12,13} and B = {13,14,15}, then (A − B) = {10,11,12} and (B − A) = {14,15}. Here, we can see (A − B) ≠ (B − A)

Complement of a Set

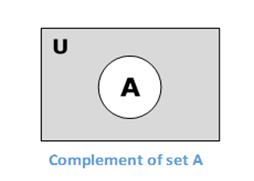
The complement of a set A (denoted by A′) is the set of elements which are not in set A. Hence, A′ = {x|x ∉ A}.

More specifically, A′ = (U−A) where U is a universal set which contains all objects.

Example − If A = {x|x belongs to set of add integers} then A′ = {y|y does not belong to set of odd integers}

Cartesian Product / Cross Product

The Cartesian product of n number of sets A1,A2,…An denoted as A1 × A2...× An can be defined as all possible ordered pairs (x1,x2,…xn) where x1 ∈ A1,x2 ∈ A2,…xn ∈ An

Example − If we take two sets A = {a,b} and B = {1,2},

The Cartesian product of A and B is written as − A × B = {(a,1),(a,2),(b,1),(b,2)}

And, the Cartesian product of B and A is written as − B × A = {(1,a),(1,b),(2,a),(2,b)}

Properties of Classical Sets

Properties on sets play an important role for obtaining the solution. Following are the different properties of classical sets −

Commutative Property

Having two sets A and B, this property states −

$$A \cup B = B \cup A$$

$$A \cap B = B \cap A$$

Associative Property

Having three sets A, B and C, this property states −

$$A\cup \left ( B\cup C \right ) = \left ( A\cup B \right )\cup C$$

$$A\cap \left ( B\cap C \right ) = \left ( A\cap B \right )\cap C$$

Distributive Property

Having three sets A, B and C, this property states −

$$A\cup \left ( B\cap C \right ) = \left ( A\cup B \right )\cap \left ( A\cup C \right )$$

$$A\cap \left ( B\cup C \right ) = \left ( A\cap B \right )\cup \left ( A\cap C \right )$$

Idempotency Property

For any set A, this property states −

$$A\cup A = A$$

$$A\cap A = A$$

Identity Property

For set A and universal set X, this property states −

$$A\cup \varphi = A$$

$$A\cap X = A$$

$$A\cap \varphi = \varphi$$

$$A\cup X = X$$

Transitive Property

Having three sets A, B and C, the property states −

If $A\subseteq B\subseteq C$, then $A\subseteq C$

Involution Property

For any set A, this property states −

$$\overline{{\overline{A}}} = A$$

De Morgan’s Law

It is a very important law and supports in proving tautologies and contradiction. This law states −

$$\overline{A\cap B} = \overline{A} \cup \overline{B}$$

$$\overline{A\cup B} = \overline{A} \cap \overline{B}$$

Previous Page Print Page