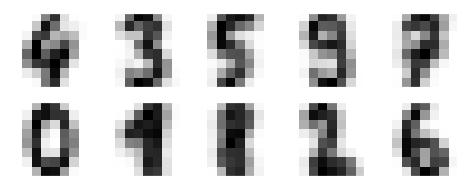ML - Clustering K-Means Algorithm

Advertisements

Previous Page
Next Page  

Introduction to K-Means Algorithm

K-means clustering algorithm computes the centroids and iterates until we it finds optimal centroid. It assumes that the number of clusters are already known. It is also called flat clustering algorithm. The number of clusters identified from data by algorithm is represented by ‘K’ in K-means.

In this algorithm, the data points are assigned to a cluster in such a manner that the sum of the squared distance between the data points and centroid would be minimum. It is to be understood that less variation within the clusters will lead to more similar data points within same cluster.

Working of K-Means Algorithm

We can understand the working of K-Means clustering algorithm with the help of following steps −

Step 1 − First, we need to specify the number of clusters, K, need to be generated by this algorithm.

Step 2 − Next, randomly select K data points and assign each data point to a cluster. In simple words, classify the data based on the number of data points.

Step 3 − Now it will compute the cluster centroids.

Step 4 − Next, keep iterating the following until we find optimal centroid which is the assignment of data points to the clusters that are not changing any more

  • 4.1 − First, the sum of squared distance between data points and centroids would be computed.

  • 4.2 − Now, we have to assign each data point to the cluster that is closer than other cluster (centroid).

  • 4.3 − At last compute the centroids for the clusters by taking the average of all data points of that cluster.

K-means follows Expectation-Maximization approach to solve the problem. The Expectation-step is used for assigning the data points to the closest cluster and the Maximization-step is used for computing the centroid of each cluster.

While working with K-means algorithm we need to take care of the following things −

  • While working with clustering algorithms including K-Means, it is recommended to standardize the data because such algorithms use distance-based measurement to determine the similarity between data points.

  • Due to the iterative nature of K-Means and random initialization of centroids, K-Means may stick in a local optimum and may not converge to global optimum. That is why it is recommended to use different initializations of centroids.

Implementation in Python

The following two examples of implementing K-Means clustering algorithm will help us in its better understanding −

Example 1

It is a simple example to understand how k-means works. In this example, we are going to first generate 2D dataset containing 4 different blobs and after that will apply k-means algorithm to see the result.

First, we will start by importing the necessary packages −

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans

The following code will generate the 2D, containing four blobs −

from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples = 400, centers = 4, cluster_std = 0.60, random_state = 0)

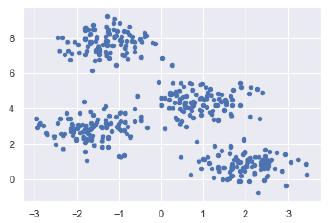
Next, the following code will help us to visualize the dataset −

plt.scatter(X[:, 0], X[:, 1], s = 20);
plt.show()

K-Mean Implementation in Python

Next, make an object of KMeans along with providing number of clusters, train the model and do the prediction as follows −

kmeans = KMeans(n_clusters = 4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)

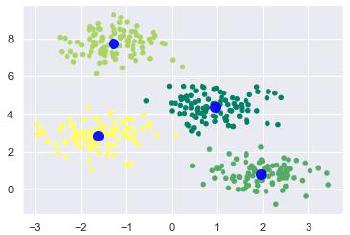
Now, with the help of following code we can plot and visualize the cluster’s centers picked by k-means Python estimator −

from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples = 400, centers = 4, cluster_std = 0.60, random_state = 0)

Next, the following code will help us to visualize the dataset −

plt.scatter(X[:, 0], X[:, 1], c = y_kmeans, s = 20, cmap = 'summer')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c = 'blue', s = 100, alpha = 0.9);
plt.show()

K-Means Python Estimator

Example 2

Let us move to another example in which we are going to apply K-means clustering on simple digits dataset. K-means will try to identify similar digits without using the original label information.

First, we will start by importing the necessary packages −

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans

Next, load the digit dataset from sklearn and make an object of it. We can also find number of rows and columns in this dataset as follows −

from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape

Output

(1797, 64)

The above output shows that this dataset is having 1797 samples with 64 features.

We can perform the clustering as we did in Example 1 above −

kmeans = KMeans(n_clusters = 10, random_state = 0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shape

Output

(10, 64)

The above output shows that K-means created 10 clusters with 64 features.

fig, ax = plt.subplots(2, 5, figsize=(8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks=[], yticks=[])
axi.imshow(center, interpolation='nearest', cmap=plt.cm.binary)

Output

As output, we will get following image showing clusters centers learned by k-means.

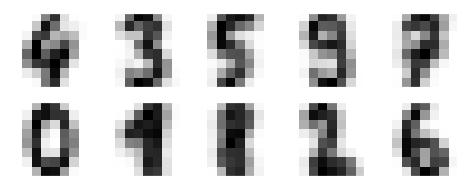
Simple Digits Dataset

The following lines of code will match the learned cluster labels with the true labels found in them −

from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
   mask = (clusters == i)
   labels[mask] = mode(digits.target[mask])[0]

Next, we can check the accuracy as follows −

from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)

Output

0.7935447968836951

The above output shows that the accuracy is around 80%.

Advantages and Disadvantages

Advantages

The following are some advantages of K-Means clustering algorithms −

  • It is very easy to understand and implement.

  • If we have large number of variables then, K-means would be faster than Hierarchical clustering.

  • On re-computation of centroids, an instance can change the cluster.

  • Tighter clusters are formed with K-means as compared to Hierarchical clustering.

Disadvantages

The following are some disadvantages of K-Means clustering algorithms −

  • It is a bit difficult to predict the number of clusters i.e. the value of k.

  • Output is strongly impacted by initial inputs like number of clusters (value of k)

  • Order of data will have strong impact on the final output.

  • It is very sensitive to rescaling. If we will rescale our data by means of normalization or standardization, then the output will completely change.

  • It is not good in doing clustering job if the clusters have a complicated geometric shape.

Applications of K-Means Clustering Algorithm

The main goals of cluster analysis are −

  • To get a meaningful intuition from the data we are working with.

  • Cluster-then-predict where different models will be built for different subgroups.

To fulfill the above-mentioned goals, K-means clustering is performing well enough. It can be used in following applications −

  • Market segmentation
  • Document Clustering
  • Image segmentation
  • Image compression
  • Customer segmentation
  • Analyzing the trend on dynamic data
Advertisements