Cryptography with Python - Quick Guide

Cryptography with Python - Overview

Cryptography is the art of communication between two users via coded messages. The science of cryptography emerged with the basic motive of providing security to the confidential messages transferred from one party to another.

Cryptography is defined as the art and science of concealing the message to introduce privacy and secrecy as recognized in information security.

Terminologies of Cryptography

The frequently used terms in cryptography are explained here −

Plain Text

The plain text message is the text which is readable and can be understood by all users. The plain text is the message which undergoes cryptography.

Cipher Text

Cipher text is the message obtained after applying cryptography on plain text.

Encryption

The process of converting plain text to cipher text is called encryption. It is also called as encoding.

Decryption

The process of converting cipher text to plain text is called decryption. It is also termed as decoding.

The diagram given below shows an illustration of the complete process of cryptography −

Characteristics of Modern Cryptography

The basic characteristics of modern cryptography are as follows −

It operates on bit sequences.
It uses mathematical algorithms for securing the information.
It requires parties interested in secure communication channel to achieve privacy.

Double Strength Encryption

Double strength encryption, also called as multiple encryption, is the process of encrypting an already encrypted text one or more times, either with the same or different algorithm/pattern.

The other names for double strength encryption include cascade encryption or cascade ciphering.

Levels of Double Strength Encryption

Double strength encryption includes various levels of encryption that are explained here under −

First layer of encryption

The cipher text is generated from the original readable message using hash algorithms and symmetric keys. Later symmetric keys are encrypted with the help of asymmetric keys. The best illustration for this pattern is combining the hash digest of the cipher text into a capsule. The receiver will compute the digest first and later decrypt the text in order to verify that text is not tampered in between.

Second layer of encryption

Second layer of encryption is the process of adding one more layer to cipher text with same or different algorithm. Usually, a 32-bit character long symmetric password is used for the same.

Third layer of encryption

In this process, the encrypted capsule is transmitted via SSL/TLS connection to the communication partner.

The following diagram shows double encryption process pictorially −

Hybrid Cryptography

Hybrid cryptography is the process of using multiple ciphers of different types together by including benefits of each of the cipher. There is one common approach which is usually followed to generate a random secret key for a symmetric cipher and then encrypt this key via asymmetric key cryptography.

Due to this pattern, the original message itself is encrypted using the symmetric cipher and then using secret key. The receiver after receiving the message decrypts the message using secret key first, using his/her own private key and then uses the specified key to decrypt the message.

Python Overview and Installation

Python is an open source scripting language which is high-level, interpreted, interactive and object-oriented. It is designed to be highly readable. The syntax of Python language is easy to understand and uses English keywords frequently.

Features of Python Language

Python provides the following major features −

Interpreted

Python is processed at runtime using the interpreter. There is no need to compile a program before execution. It is similar to PERL and PHP.

Object-Oriented

Python follows object-oriented style and design patterns. It includes class definition with various features like encapsulation and polymorphism.

Key Points of Python Language

The key points of Python programming language are as follows −

It includes functional and structured programming and methods as well as object oriented programming methods.
It can be used as a scripting language or as a programming language.
It includes automatic garbage collection.
It includes high-level dynamic data types and supports various dynamic type checking.
Python includes a feature of integration with C, C++ and languages like Java.

The download link for Python language is as follows − www.python.org/downloadsIt includes packages for various operating systems like Windows, MacOS and Linux distributions.

Python Strings

The basic declaration of strings is shown below −

str = 'Hello World!'

Python Lists

The lists of python can be declared as compound data types, separated by commas and enclosed within square brackets ([]).

list = [ 'abcd', 786 , 2.23, 'john', 70.2 ]
tinylist = [123, 'john']

Python Tuples

A tuple is dynamic data type of Python which consists of number of values separated by commas. Tuples are enclosed with parentheses.

tinytuple = (123, 'john')

Python Dictionary

Python dictionary is a type of hash table. A dictionary key can be almost any data type of Python, which are usually numbers or strings.

tinydict = {'name': 'omkar','code':6734, 'dept': 'sales'}

Cryptography Packages

Python includes a package called cryptography which provides cryptographic recipes and primitives. It supports Python 2.7, Python 3.4+, and PyPy 5.3+. The basic installation of cryptography package is achieved through following command −

pip install cryptography

There are various packages with both high level recipes and low level interfaces to common cryptographic algorithms such as symmetric ciphers, message digests and key derivation functions.

Throughout this tutorial, we will be using various packages of Python for implementation of cryptographic algorithms.

Cryptography with Python - Reverse Cipher

The previous chapter gave you an overview of installation of Python on your local computer. In this chapter you will learn in detail about reverse cipher and its coding.

Algorithm of Reverse Cipher

The algorithm of reverse cipher holds the following features −

Reverse Cipher uses a pattern of reversing the string of plain text to convert as cipher text.
The process of encryption and decryption is same.
To decrypt cipher text, the user simply needs to reverse the cipher text to get the plain text.

Drawback

The major drawback of reverse cipher is that it is very weak. A hacker can easily break the cipher text to get the original message. Hence, reverse cipher is not considered as good option to maintain secure communication channel,.

Example

Consider an example where the statement This is program to explain reverse cipher is to be implemented with reverse cipher algorithm. The following python code uses the algorithm to obtain the output.

message = 'This is program to explain reverse cipher.'
translated = '' #cipher text is stored in this variable
i = len(message) - 1

while i >= 0:
   translated = translated + message[i]
   i = i - 1
print(“The cipher text is : “, translated)

Output

You can see the reversed text, that is the output as shown in the following image −

Explanation

Plain text is stored in the variable message and the translated variable is used to store the cipher text created.
The length of plain text is calculated using for loop and with help of index number. The characters are stored in cipher text variable translated which is printed in the last line.

Cryptography with Python - Caesar Cipher

In the last chapter, we have dealt with reverse cipher. This chapter talks about Caesar cipher in detail.

Algorithm of Caesar Cipher

The algorithm of Caesar cipher holds the following features −

Caesar Cipher Technique is the simple and easy method of encryption technique.
It is simple type of substitution cipher.
Each letter of plain text is replaced by a letter with some fixed number of positions down with alphabet.

The following diagram depicts the working of Caesar cipher algorithm implementation −

The program implementation of Caesar cipher algorithm is as follows −

def encrypt(text,s):
result = ""
   # transverse the plain text
   for i in range(len(text)):
      char = text[i]
      # Encrypt uppercase characters in plain text
      
      if (char.isupper()):
         result += chr((ord(char) + s-65) % 26 + 65)
      # Encrypt lowercase characters in plain text
      else:
         result += chr((ord(char) + s - 97) % 26 + 97)
      return result
#check the above function
text = "CEASER CIPHER DEMO"
s = 4

print "Plain Text : " + text
print "Shift pattern : " + str(s)
print "Cipher: " + encrypt(text,s)

Output

You can see the Caesar cipher, that is the output as shown in the following image −

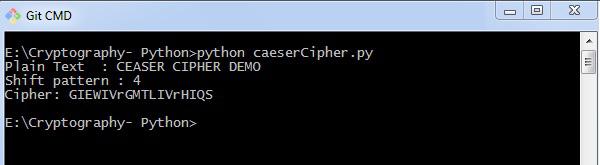
Explanation

The plain text character is traversed one at a time.

For each character in the given plain text, transform the given character as per the rule depending on the procedure of encryption and decryption of text.
After the steps is followed, a new string is generated which is referred as cipher text.

Hacking of Caesar Cipher Algorithm

The cipher text can be hacked with various possibilities. One of such possibility is Brute Force Technique, which involves trying every possible decryption key. This technique does not demand much effort and is relatively simple for a hacker.

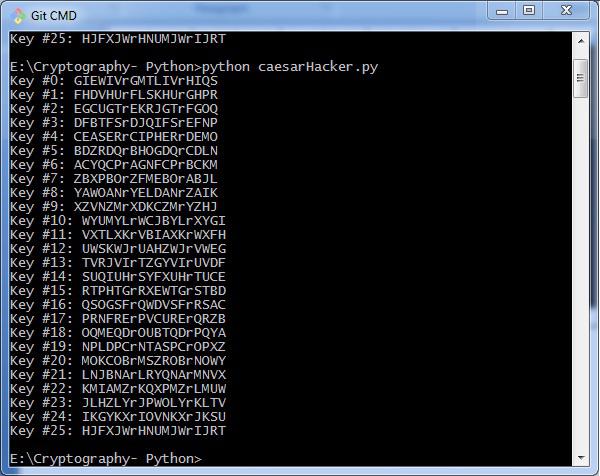
The program implementation for hacking Caesar cipher algorithm is as follows −

message = 'GIEWIVrGMTLIVrHIQS' #encrypted message
LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'

for key in range(len(LETTERS)):
   translated = ''
   for symbol in message:
      if symbol in LETTERS:
         num = LETTERS.find(symbol)
         num = num - key
         if num < 0:
            num = num + len(LETTERS)
         translated = translated + LETTERS[num]
      else:
         translated = translated + symbol
print('Hacking key #%s: %s' % (key, translated))

Consider the cipher text encrypted in the previous example. Then, the output with possible hacking methods with the key and using brute force attack technique is as follows −

Cryptography with Python - ROT13 Algorithm

Till now, you have learnt about reverse cipher and Caesar cipher algorithms. Now, let us discuss the ROT13 algorithm and its implementation.

Explanation of ROT13 Algorithm

ROT13 cipher refers to the abbreviated form Rotate by 13 places. It is a special case of Caesar Cipher in which shift is always 13. Every letter is shifted by 13 places to encrypt or decrypt the message.

Example

The following diagram explains the ROT13 algorithm process pictorially −

Program Code

The program implementation of ROT13 algorithm is as follows −

from string import maketrans

rot13trans = maketrans('ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz', 
   'NOPQRSTUVWXYZABCDEFGHIJKLMnopqrstuvwxyzabcdefghijklm')

# Function to translate plain text
def rot13(text):
   return text.translate(rot13trans)
def main():
   txt = "ROT13 Algorithm"
   print rot13(txt)
	
if __name__ == "__main__":
   main()

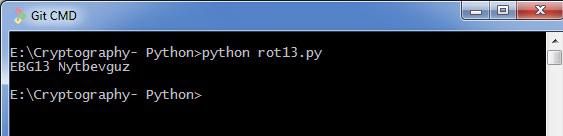
You can see the ROT13 output as shown in the following image −

Drawback

The ROT13 algorithm uses 13 shifts. Therefore, it is very easy to shift the characters in the reverse manner to decrypt the cipher text.

Analysis of ROT13 Algorithm

ROT13 cipher algorithm is considered as special case of Caesar Cipher. It is not a very secure algorithm and can be broken easily with frequency analysis or by just trying possible 25 keys whereas ROT13 can be broken by shifting 13 places. Therefore, it does not include any practical use.

Transposition Cipher

Transposition Cipher is a cryptographic algorithm where the order of alphabets in the plaintext is rearranged to form a cipher text. In this process, the actual plain text alphabets are not included.

Example

A simple example for a transposition cipher is columnar transposition cipher where each character in the plain text is written horizontally with specified alphabet width. The cipher is written vertically, which creates an entirely different cipher text.

Consider the plain text hello world, and let us apply the simple columnar transposition technique as shown below

The plain text characters are placed horizontally and the cipher text is created with vertical format as : holewdlo lr. Now, the receiver has to use the same table to decrypt the cipher text to plain text.

Code

The following program code demonstrates the basic implementation of columnar transposition technique −

def split_len(seq, length):
   return [seq[i:i + length] for i in range(0, len(seq), length)]
def encode(key, plaintext):
   order = {
      int(val): num for num, val in enumerate(key)
   }
ciphertext = ''

for index in sorted(order.keys()):
   for part in split_len(plaintext, len(key)):
      try:ciphertext += part[order[index]]
         except IndexError:
            continue
   return ciphertext
print(encode('3214', 'HELLO'))

Explanation

Using the function split_len(), we can split the plain text characters, which can be placed in columnar or row format.
encode method helps to create cipher text with key specifying the number of columns and prints the cipher text by reading characters through each column.

Output

The program code for the basic implementation of columnar transposition technique gives the following output −

Note − Cryptanalysts observed a significant improvement in crypto security when transposition technique is performed. They also noted that re-encrypting the cipher text using same transposition cipher creates better security.

Encryption of Transposition Cipher

In the previous chapter, we have learnt about Transposition Cipher. In this chapter, let us discuss its encryption.

Pyperclip

The main usage of pyperclip plugin in Python programming language is to perform cross platform module for copying and pasting text to the clipboard. You can install python pyperclip module using the command as shown

pip install pyperclip

If the requirement already exists in the system, you can see the following output −

Code

The python code for encrypting transposition cipher in which pyperclip is the main module is as shown below −

import pyperclip
def main():
   myMessage = 'Transposition Cipher'
   myKey = 10
   ciphertext = encryptMessage(myKey, myMessage)
   
   print("Cipher Text is")
   print(ciphertext + '|')
   pyperclip.copy(ciphertext)

def encryptMessage(key, message):
   ciphertext = [''] * key
   
   for col in range(key):
      position = col
      while position < len(message):
         ciphertext[col] += message[position]
			position += key
      return ''.join(ciphertext) #Cipher text
if __name__ == '__main__':
   main()

Output

The program code for encrypting transposition cipher in which pyperclip is the main module gives the following output −

Explanation

The function main() calls the encryptMessage() which includes the procedure for splitting the characters using len function and iterating them in a columnar format.
The main function is initialized at the end to get the appropriate output.

Decryption of Transposition Cipher

In this chapter, you will learn the procedure for decrypting the transposition cipher.

Code

Observe the following code for a better understanding of decrypting a transposition cipher. The cipher text for message Transposition Cipher with key as 6 is fetched as Toners raiCntisippoh.

import math, pyperclip
def main():
   myMessage= 'Toners raiCntisippoh'
   myKey = 6
   plaintext = decryptMessage(myKey, myMessage)
   
   print("The plain text is")
   print('Transposition Cipher')

def decryptMessage(key, message):
   numOfColumns = math.ceil(len(message) / key)
   numOfRows = key
   numOfShadedBoxes = (numOfColumns * numOfRows) - len(message)
   plaintext = float('') * numOfColumns
   col = 0
   row = 0
   
   for symbol in message:
      plaintext[col] += symbol
      col += 1
      if (col == numOfColumns) or (col == numOfColumns - 1 and row >= numOfRows - numOfShadedBoxes):
         col = 0 row += 1 return ''.join(plaintext)
if __name__ == '__main__':
   main()

Explanation

The cipher text and the mentioned key are the two values taken as input parameters for decoding or decrypting the cipher text in reverse technique by placing characters in a column format and reading them in a horizontal manner.

You can place letters in a column format and later combined or concatenate them together using the following piece of code −

for symbol in message:
   plaintext[col] += symbol
   col += 1
   
   if (col == numOfColumns) or (col == numOfColumns - 1 and row >= numOfRows - numOfShadedBoxes):
   col = 0
   row += 1
return ''.join(plaintext)

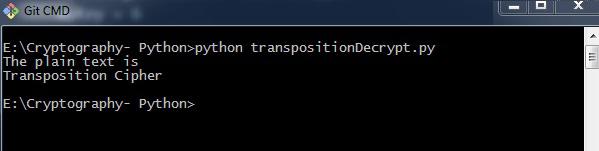
Output

The program code for decrypting transposition cipher gives the following output −

Encryption of files

In Python, it is possible to encrypt and decrypt files before transmitting to a communication channel. For this, you will have to use the plugin PyCrypto. You can installation this plugin using the command given below.

pip install pycrypto

Code

The program code for encrypting the file with password protector is mentioned below −

# =================Other Configuration================
# Usages :
usage = "usage: %prog [options] "
# Version
Version="%prog 0.0.1"
# ====================================================
# Import Modules
import optparse, sys,os
from toolkit import processor as ps
def main():
   parser = optparse.OptionParser(usage = usage,version = Version)
   parser.add_option(
      '-i','--input',type = 'string',dest = 'inputfile',
      help = "File Input Path For Encryption", default = None)
   
   parser.add_option(
      '-o','--output',type = "string",dest = 'outputfile',
      help = "File Output Path For Saving Encrypter Cipher",default = ".")
	
   parser.add_option(
      '-p','--password',type = "string",dest = 'password',
      help = "Provide Password For Encrypting File",default = None)
	
   parser.add_option(
      '-p','--password',type = "string",dest = 'password',
      help = "Provide Password For Encrypting File",default = None)
	
   (options, args)= parser.parse_args()
	
   # Input Conditions Checkings
   if not options.inputfile or not os.path.isfile(options.inputfile):
      print " [Error] Please Specify Input File Path"
      exit(0)
   if not options.outputfile or not os.path.isdir(options.outputfile):
      print " [Error] Please Specify Output Path"
      exit(0)
   if not options.password:
      print " [Error] No Password Input"
      exit(0)
   inputfile = options.inputfile

   outputfile = os.path.join(
      options.outputfile,os.path.basename(options.inputfile).split('.')[0]+'.ssb')
   password = options.password
   base = os.path.basename(inputfile).split('.')[1]
   work = "E"

   ps.FileCipher(inputfile,outputfile,password,work)
   return

   if __name__ == '__main__':
   main()

You can use the following command to execute the encryption process along with password −

python pyfilecipher-encrypt.py -i file_path_for_encryption -o output_path -p password

Output

You can observe the following output when you execute the code given above −

Explanation

The passwords are generated using MD5 hash algorithm and the values are stored in simply safe backup files in Windows system, which includes the values as displayed below −

Decryption of files

In this chapter, let us discuss decryption of files in cryptography using Python. Note that for decryption process, we will follow the same procedure, but instead of specifying the output path, we will focus on input path or the necessary file which is encrypted.

Code

The following is a sample code for decrypting files in cryptography using Python −

#!/usr/bin/python
# ---------------- READ ME ---------------------------------------------
# This Script is Created Only For Practise And Educational Purpose Only
# This Script Is Created For http://bitforestinfo.blogspot.in
# This Script is Written By
#
#
##################################################
######## Please Don't Remove Author Name #########
############### Thanks ###########################
##################################################
#
#
# =================Other Configuration================
# Usages :
usage = "usage: %prog [options] "
# Version
Version="%prog 0.0.1"
# ====================================================
# Import Modules
import optparse, sys,os
from toolkit import processor as ps
def main():
   parser = optparse.OptionParser(usage = usage,version = Version)
   parser.add_option(
      '-i','--input',type = 'string',dest = 'inputfile',
      help = "File Input Path For Encryption", default = None)
   
   parser.add_option(
      '-o','--output',type = "string",dest = 'outputfile',
      help = "File Output Path For Saving Encrypter Cipher",default = ".")
   
   parser.add_option(
      '-p','--password',type = "string",dest = 'password',
      help = "Provide Password For Encrypting File",default = None)
      (options, args) =  parser.parse_args()
      # Input Conditions Checkings
      if not options.inputfile or not os.path.isfile(options.inputfile):
         print " [Error] Please Specify Input File Path"
         exit(0)
      if not options.outputfile or not os.path.isdir(options.outputfile):
         print " [Error] Please Specify Output Path"
         exit(0)
      if not options.password:
         print " [Error] No
         exit(0)
      inputfile = options.inputfile
      outputfile = options.outputfile
      password = options.password
      work = "D"
      ps.FileCipher(inputfile,outputfile,password,work)
      return
if __name__ == '__main__':
   main()

You can use the following command for executing the above code −

python pyfilecipher-decrypt.py -i encrypted_file_path -p password

Output

You can observe the following code when you execute the command shown above −

Note − The output specifies the hash values before encryption and after decryption, which keeps a note that the same file is encrypted and the process was successful.

Base64 Encoding and Decoding

Base64 encoding converts the binary data into text format, which is passed through communication channel where a user can handle text safely. Base64 is also called as Privacy enhanced Electronic mail (PEM) and is primarily used in email encryption process.

Python includes a module called BASE64 which includes two primary functions as given below −

base64.decode(input, output) − It decodes the input value parameter specified and stores the decoded output as an object.
Base64.encode(input, output) − It encodes the input value parameter specified and stores the decoded output as an object.

Program for Encoding

You can use the following piece of code to perform base64 encoding −

import base64
encoded_data = base64.b64encode("Encode this text")

print("Encoded text with base 64 is")
print(encoded_data)

Output

The code for base64 encoding gives you the following output −

Program for Decoding

You can use the following piece of code to perform base64 decoding −

import base64
decoded_data = base64.b64decode("RW5jb2RlIHRoaXMgdGV4dA==")

print("decoded text is ")
print(decoded_data)

Output

The code for base64 decoding gives you the following output −

Difference between ASCII and base64

You can observe the following differences when you work on ASCII and base64 for encoding data −

When you encode text in ASCII, you start with a text string and convert it to a sequence of bytes.
When you encode data in Base64, you start with a sequence of bytes and convert it to a text string.

Drawback

Base64 algorithm is usually used to store passwords in database. The major drawback is that each decoded word can be encoded easily through any online tool and intruders can easily get the information.

Cryptography with Python - XOR Process

In this chapter, let us understand the XOR process along with its coding in Python.

Algorithm

XOR algorithm of encryption and decryption converts the plain text in the format ASCII bytes and uses XOR procedure to convert it to a specified byte. It offers the following advantages to its users −

Fast computation
No difference marked in left and right side
Easy to understand and analyze

Code

You can use the following piece of code to perform XOR process −

def xor_crypt_string(data, key = 'awesomepassword', encode = False, decode = False):
   from itertools import izip, cycle
   import base64
   
   if decode:
      data = base64.decodestring(data)
   xored = ''.join(chr(ord(x) ^ ord(y)) for (x,y) in izip(data, cycle(key)))
   
   if encode:
      return base64.encodestring(xored).strip()
   return xored
secret_data = "XOR procedure"

print("The cipher text is")
print xor_crypt_string(secret_data, encode = True)
print("The plain text fetched")
print xor_crypt_string(xor_crypt_string(secret_data, encode = True), decode = True)

Output

The code for XOR process gives you the following output −

Explanation

The function xor_crypt_string() includes a parameter to specify mode of encode and decode and also the string value.
The basic functions are taken with base64 modules which follows the XOR procedure/ operation to encrypt or decrypt the plain text/ cipher text.

Note − XOR encryption is used to encrypt data and is hard to crack by brute-force method, that is by generating random encrypting keys to match with the correct cipher text.

Multiplicative Cipher

While using Caesar cipher technique, encrypting and decrypting symbols involves converting the values into numbers with a simple basic procedure of addition or subtraction.

If multiplication is used to convert to cipher text, it is called a wrap-around situation. Consider the letters and the associated numbers to be used as shown below −

The numbers will be used for multiplication procedure and the associated key is 7. The basic formula to be used in such a scenario to generate a multiplicative cipher is as follows −

(Alphabet Number * key)mod(total number of alphabets)

The number fetched through output is mapped in the table mentioned above and the corresponding letter is taken as the encrypted letter.

The basic modulation function of a multiplicative cipher in Python is as follows −

def unshift(key, ch):
   offset = ord(ch) - ASC_A
   return chr(((key[0] * (offset + key[1])) % WIDTH) + ASC_A)

Note − The advantage with a multiplicative cipher is that it can work with very large keys like 8,953,851. It would take quite a long time for a computer to brute-force through a majority of nine million keys.

Cryptography with Python - Affine Cipher

Affine Cipher is the combination of Multiplicative Cipher and Caesar Cipher algorithm. The basic implementation of affine cipher is as shown in the image below −

In this chapter, we will implement affine cipher by creating its corresponding class that includes two basic functions for encryption and decryption.

Code

You can use the following code to implement an affine cipher −

class Affine(object):
   DIE = 128
   KEY = (7, 3, 55)
   def __init__(self):
      pass
   def encryptChar(self, char):
      K1, K2, kI = self.KEY
      return chr((K1 * ord(char) + K2) % self.DIE)
		
   def encrypt(self, string):
      return "".join(map(self.encryptChar, string))
   
   def decryptChar(self, char):
      K1, K2, KI = self.KEY
      return chr(KI * (ord(char) - K2) % self.DIE)
   
   def decrypt(self, string):
      return "".join(map(self.decryptChar, string))
		affine = Affine()
print affine.encrypt('Affine Cipher')
print affine.decrypt('*18?FMT')

Output

You can observe the following output when you implement an affine cipher −

The output displays the encrypted message for the plain text message Affine Cipher and decrypted message for the message sent as input abcdefg.

Hacking Monoalphabetic Cipher

In this chapter, you will learn about monoalphabetic cipher and its hacking using Python.

Monoalphabetic Cipher

A Monoalphabetic cipher uses a fixed substitution for encrypting the entire message. A monoalphabetic cipher using a Python dictionary with JSON objects is shown here −

monoalpha_cipher = {
   'a': 'm',
   'b': 'n',
   'c': 'b',
   'd': 'v',
   'e': 'c',
   'f': 'x',
   'g': 'z',
   'h': 'a',
   'i': 's',
   'j': 'd',
   'k': 'f',
   'l': 'g',
   'm': 'h',
   'n': 'j',
   'o': 'k',
   'p': 'l',
   'q': 'p',
   'r': 'o',
   's': 'i',
   't': 'u',
   'u': 'y',
   'v': 't',
   'w': 'r',
   'x': 'e',
   'y': 'w',
   'z': 'q',
	' ': ' ',
}

With help of this dictionary, we can encrypt the letters with the associated letters as values in JSON object. The following program creates a monoalphabetic program as a class representation which includes all the functions of encryption and decryption.

from string import letters, digits
from random import shuffle

def random_monoalpha_cipher(pool = None):
   if pool is None:
      pool = letters + digits
   original_pool = list(pool)
   shuffled_pool = list(pool)
   shuffle(shuffled_pool)
   return dict(zip(original_pool, shuffled_pool))

def inverse_monoalpha_cipher(monoalpha_cipher):
   inverse_monoalpha = {}
   for key, value in monoalpha_cipher.iteritems():
      inverse_monoalpha[value] = key
   return inverse_monoalpha

def encrypt_with_monoalpha(message, monoalpha_cipher):
   encrypted_message = []
   for letter in message:
      encrypted_message.append(monoalpha_cipher.get(letter, letter))
   return ''.join(encrypted_message)

def decrypt_with_monoalpha(encrypted_message, monoalpha_cipher):
   return encrypt_with_monoalpha(
      encrypted_message,
      inverse_monoalpha_cipher(monoalpha_cipher)
   )

This file is called later to implement the encryption and decryption process of Monoalphabetic cipher which is mentioned as below −

import monoalphabeticCipher as mc

cipher = mc.random_monoalpha_cipher()
print(cipher)
encrypted = mc.encrypt_with_monoalpha('Hello all you hackers out there!', cipher)
decrypted = mc.decrypt_with_monoalpha('sXGGt SGG Nt0 HSrLXFC t0U UHXFX!', cipher)

print(encrypted)
print(decrypted)

Output

You can observe the following output when you implement the code given above −

Thus, you can hack a monoalphabetic cipher with specified key value pair which cracks the cipher text to actual plain text.

Simple Substitution Cipher

Simple substitution cipher is the most commonly used cipher and includes an algorithm of substituting every plain text character for every cipher text character. In this process, alphabets are jumbled in comparison with Caesar cipher algorithm.

Example

Keys for a simple substitution cipher usually consists of 26 letters. An example key is −

plain alphabet : abcdefghijklmnopqrstuvwxyz
cipher alphabet: phqgiumeaylnofdxjkrcvstzwb

An example encryption using the above key is−

plaintext : defend the east wall of the castle
ciphertext: giuifg cei iprc tpnn du cei qprcni

The following code shows a program to implement simple substitution cipher −

import random, sys

LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
def main():
   message = ''
   if len(sys.argv) > 1:
      with open(sys.argv[1], 'r') as f:
         message = f.read()
   else:
      message = raw_input("Enter your message: ")
   mode = raw_input("E for Encrypt, D for Decrypt: ")
   key = ''
   
   while checkKey(key) is False:
      key = raw_input("Enter 26 ALPHA key (leave blank for random key): ")
      if key == '':
         key = getRandomKey()
      if checkKey(key) is False:
		print('There is an error in the key or symbol set.')
   translated = translateMessage(message, key, mode)
   print('Using key: %s' % (key))
   
   if len(sys.argv) > 1:
      fileOut = 'enc.' + sys.argv[1]
      with open(fileOut, 'w') as f:
         f.write(translated)
      print('Success! File written to: %s' % (fileOut))
   else: print('Result: ' + translated)

# Store the key into list, sort it, convert back, compare to alphabet.
def checkKey(key):
   keyString = ''.join(sorted(list(key)))
   return keyString == LETTERS
def translateMessage(message, key, mode):
   translated = ''
   charsA = LETTERS
   charsB = key
   
   # If decrypt mode is detected, swap A and B
   if mode == 'D':
      charsA, charsB = charsB, charsA
   for symbol in message:
      if symbol.upper() in charsA:
         symIndex = charsA.find(symbol.upper())
         if symbol.isupper():
            translated += charsB[symIndex].upper()
         else:
            translated += charsB[symIndex].lower()
				else:
               translated += symbol
         return translated
def getRandomKey():
   randomList = list(LETTERS)
   random.shuffle(randomList)
   return ''.join(randomList)
if __name__ == '__main__':
   main()

Output

You can observe the following output when you implement the code given above −

Testing of Simple Substitution Cipher

In this chapter, we will focus on testing substitution cipher using various methods, which helps to generate random strings as given below −

import random, string, substitution
def main():
   for i in range(1000):
      key = substitution.getRandomKey()
      message = random_string()
      print('Test %s: String: "%s.."' % (i + 1, message[:50]))
      print("Key: " + key)
      encrypted = substitution.translateMessage(message, key, 'E')
      decrypted = substitution.translateMessage(encrypted, key, 'D')
      
      if decrypted != message:
         print('ERROR: Decrypted: "%s" Key: %s' % (decrypted, key))
         sys.exit()
      print('Substutition test passed!')

def random_string(size = 5000, chars = string.ascii_letters + string.digits):
   return ''.join(random.choice(chars) for _ in range(size))
if __name__ == '__main__':
   main()

Output

You can observe the output as randomly generated strings which helps in generating random plain text messages, as shown below −

After the test is successfully completed, we can observe the output message Substitution test passed!.

Thus, you can hack a substitution cipher in the systematic manner.

Decryption of Simple Substitution Cipher

In this chapter, you can learn about simple implementation of substitution cipher which displays the encrypted and decrypted message as per the logic used in simple substitution cipher technique. This can be considered as an alternative approach of coding.

Code

You can use the following code to perform decryption using simple substitution cipher −

import random
chars = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ' + \
   'abcdefghijklmnopqrstuvwxyz' + \
   '0123456789' + \
   ':.;,?!@#$%&()+=-*/_<> []{}`~^"\'\\'

def generate_key():
   """Generate an key for our cipher"""
   shuffled = sorted(chars, key=lambda k: random.random())
   return dict(zip(chars, shuffled))

def encrypt(key, plaintext):
   """Encrypt the string and return the ciphertext"""
   return ''.join(key[l] for l in plaintext)

def decrypt(key, ciphertext):
   """Decrypt the string and return the plaintext"""
   flipped = {v: k for k, v in key.items()}
   return ''.join(flipped[l] for l in ciphertext)

def show_result(plaintext):
   """Generate a resulting cipher with elements shown"""
   key = generate_key()
   encrypted = encrypt(key, plaintext)
   decrypted = decrypt(key, encrypted)
   
   print 'Key: %s' % key
	print 'Plaintext: %s' % plaintext
   print 'Encrypted: %s' % encrypted
   print 'Decrypted: %s' % decrypted
show_result('Hello World. This is demo of substitution cipher')

Output

The above code gives you the output as shown here −

Python Modules of Cryptography

In this chapter, you will learn in detail about various modules of cryptography in Python.

Cryptography Module

It includes all the recipes and primitives, and provides a high level interface of coding in Python. You can install cryptography module using the following command −

pip install cryptography

Code

You can use the following code to implement the cryptography module −

from cryptography.fernet import Fernet
key = Fernet.generate_key()
cipher_suite = Fernet(key)
cipher_text = cipher_suite.encrypt("This example is used to demonstrate cryptography module")
plain_text = cipher_suite.decrypt(cipher_text)

Output

The code given above produces the following output −

The code given here is used to verify the password and creating its hash. It also includes logic for verifying the password for authentication purpose.

import uuid
import hashlib

def hash_password(password):
   # uuid is used to generate a random number of the specified password
   salt = uuid.uuid4().hex
   return hashlib.sha256(salt.encode() + password.encode()).hexdigest() + ':' + salt

def check_password(hashed_password, user_password):
   password, salt = hashed_password.split(':')
   return password == hashlib.sha256(salt.encode() + user_password.encode()).hexdigest()

new_pass = input('Please enter a password: ')
hashed_password = hash_password(new_pass)
print('The string to store in the db is: ' + hashed_password)
old_pass = input('Now please enter the password again to check: ')

if check_password(hashed_password, old_pass):
   print('You entered the right password')
else:
   print('Passwords do not match')

Output

Scenario 1 − If you have entered a correct password, you can find the following output −

Scenario 2 − If we enter wrong password, you can find the following output −

Explanation

Hashlib package is used for storing passwords in a database. In this program, salt is used which adds a random sequence to the password string before implementing the hash function.

Understanding Vignere Cipher

Vignere Cipher includes a twist with Caesar Cipher algorithm used for encryption and decryption. Vignere Cipher works similar to Caesar Cipher algorithm with only one major distinction: Caesar Cipher includes algorithm for one-character shift, whereas Vignere Cipher includes key with multiple alphabets shift.

Mathematical Equation

For encryption the mathematical equation is as follows −

$$E_{k}\left ( M{_{i{}}} \right ) = \left ( M_{i}+K_{i} \right )\;\;\; mod \;\; 26$$

For decryption the mathematical equation is as follows −

$$D_{k}\left ( C{_{i{}}} \right ) = \left ( C_{i}-K_{i} \right )\;\;\; mod \;\; 26$$

Vignere cipher uses more than one set of substitutions, and hence it is also referred as polyalphabetic cipher. Vignere Cipher will use a letter key instead of a numeric key representation: Letter A will be used for key 0, letter B for key 1 and so on. Numbers of the letters before and after encryption process is shown below −

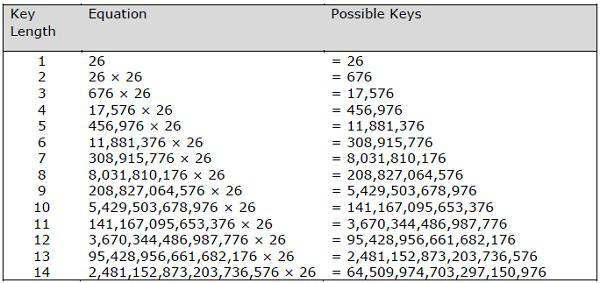
The possible combination of number of possible keys based on Vignere key length is given as follows, which gives the result of how secure is Vignere Cipher Algorithm −

Vignere Tableau

The tableau used for Vignere cipher is as shown below −

Implementing Vignere Cipher

In this chapter, let us understand how to implement Vignere cipher. Consider the text This is basic implementation of Vignere Cipher is to be encoded and the key used is PIZZA.

Code

You can use the following code to implement a Vignere cipher in Python −

import pyperclip

LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
def main():
   myMessage = "This is basic implementation of Vignere Cipher"
   myKey = 'PIZZA'
   myMode = 'encrypt'
   
   if myMode == 'encrypt':
      translated = encryptMessage(myKey, myMessage)
   elif myMode == 'decrypt':
      translated = decryptMessage(myKey, myMessage)
   
   print('%sed message:' % (myMode.title()))
   print(translated)
   print()
def encryptMessage(key, message):
   return translateMessage(key, message, 'encrypt')
def decryptMessage(key, message):
   return translateMessage(key, message, 'decrypt')
def translateMessage(key, message, mode):
   translated = [] # stores the encrypted/decrypted message string
   keyIndex = 0
   key = key.upper()
   
   for symbol in message:
      num = LETTERS.find(symbol.upper())
      if num != -1:
         if mode == 'encrypt':
            num += LETTERS.find(key[keyIndex])
				elif mode == 'decrypt':
               num -= LETTERS.find(key[keyIndex])
            num %= len(LETTERS)
            
            if symbol.isupper():
               translated.append(LETTERS[num])
            elif symbol.islower():
               translated.append(LETTERS[num].lower())
            keyIndex += 1
            
            if keyIndex == len(key):
               keyIndex = 0
         else:
            translated.append(symbol)
      return ''.join(translated)
if __name__ == '__main__':
   main()

Output

You can observe the following output when you implement the code given above −

The possible combinations of hacking the Vignere cipher is next to impossible. Hence, it is considered as a secure encryption mode.

One Time Pad Cipher

One-time pad cipher is a type of Vignere cipher which includes the following features −

It is an unbreakable cipher.
The key is exactly same as the length of message which is encrypted.
The key is made up of random symbols.
As the name suggests, key is used one time only and never used again for any other message to be encrypted.

Due to this, encrypted message will be vulnerable to attack for a cryptanalyst. The key used for a one-time pad cipher is called pad, as it is printed on pads of paper.

Why is it Unbreakable?

The key is unbreakable owing to the following features −

The key is as long as the given message.
The key is truly random and specially auto-generated.
Key and plain text calculated as modulo 10/26/2.
Each key should be used once and destroyed by both sender and receiver.
There should be two copies of key: one with the sender and other with the receiver.

Encryption

To encrypt a letter, a user needs to write a key underneath the plaintext. The plaintext letter is placed on the top and the key letter on the left. The cross section achieved between two letters is the plain text. It is described in the example below −

Decryption

To decrypt a letter, user takes the key letter on the left and finds cipher text letter in that row. The plain text letter is placed at the top of the column where the user can find the cipher text letter.

Implementation of One Time Pad Cipher

Python includes a hacky implementation module for one-time-pad cipher implementation. The package name is called One-Time-Pad which includes a command line encryption tool that uses encryption mechanism similar to the one-time pad cipher algorithm.

Installation

You can use the following command to install this module −

pip install onetimepad

If you wish to use it from the command-line, run the following command −

onetimepad

Code

The following code helps to generate a one-time pad cipher −

import onetimepad

cipher = onetimepad.encrypt('One Time Cipher', 'random')
print("Cipher text is ")
print(cipher)
print("Plain text is ")
msg = onetimepad.decrypt(cipher, 'random')

print(msg)

Output

You can observe the following output when you run the code given above −

Note − The encrypted message is very easy to crack if the length of the key is less than the length of message (plain text).

In any case, the key is not necessarily random, which makes one-time pad cipher as a worth tool.

Symmetric and Asymmetric Cryptography

In this chapter, let us discuss in detail about symmetric and asymmetric cryptography.

Symmetric Cryptography

In this type, the encryption and decryption process uses the same key. It is also called as secret key cryptography. The main features of symmetric cryptography are as follows −

It is simpler and faster.
The two parties exchange the key in a secure way.

Drawback

The major drawback of symmetric cryptography is that if the key is leaked to the intruder, the message can be easily changed and this is considered as a risk factor.

Data Encryption Standard (DES)

The most popular symmetric key algorithm is Data Encryption Standard (DES) and Python includes a package which includes the logic behind DES algorithm.

Installation

The command for installation of DES package pyDES in Python is −

pip install pyDES

Simple program implementation of DES algorithm is as follows −

import pyDes

data = "DES Algorithm Implementation"
k = pyDes.des("DESCRYPT", pyDes.CBC, "\0\0\0\0\0\0\0\0", pad=None, padmode=pyDes.PAD_PKCS5)
d = k.encrypt(data)

print "Encrypted: %r" % d
print "Decrypted: %r" % k.decrypt(d)
assert k.decrypt(d) == data

It calls for the variable padmode which fetches all the packages as per DES algorithm implementation and follows encryption and decryption in a specified manner.

Output

You can see the following output as a result of the code given above −

Asymmetric Cryptography

It is also called as public key cryptography. It works in the reverse way of symmetric cryptography. This implies that it requires two keys: one for encryption and other for decryption. The public key is used for encrypting and the private key is used for decrypting.

Drawback

Due to its key length, it contributes lower encryption speed.
Key management is crucial.

The following program code in Python illustrates the working of asymmetric cryptography using RSA algorithm and its implementation −

from Crypto import Random
from Crypto.PublicKey import RSA
import base64

def generate_keys():
   # key length must be a multiple of 256 and >= 1024
   modulus_length = 256*4
   privatekey = RSA.generate(modulus_length, Random.new().read)
   publickey = privatekey.publickey()
   return privatekey, publickey

def encrypt_message(a_message , publickey):
   encrypted_msg = publickey.encrypt(a_message, 32)[0]
   encoded_encrypted_msg = base64.b64encode(encrypted_msg)
   return encoded_encrypted_msg

def decrypt_message(encoded_encrypted_msg, privatekey):
   decoded_encrypted_msg = base64.b64decode(encoded_encrypted_msg)
   decoded_decrypted_msg = privatekey.decrypt(decoded_encrypted_msg)
   return decoded_decrypted_msg

a_message = "This is the illustration of RSA algorithm of asymmetric cryptography"
privatekey , publickey = generate_keys()
encrypted_msg = encrypt_message(a_message , publickey)
decrypted_msg = decrypt_message(encrypted_msg, privatekey)

print "%s - (%d)" % (privatekey.exportKey() , len(privatekey.exportKey()))
print "%s - (%d)" % (publickey.exportKey() , len(publickey.exportKey()))
print " Original content: %s - (%d)" % (a_message, len(a_message))
print "Encrypted message: %s - (%d)" % (encrypted_msg, len(encrypted_msg))
print "Decrypted message: %s - (%d)" % (decrypted_msg, len(decrypted_msg))

Output

You can find the following output when you execute the code given above −

Understanding RSA Algorithm

RSA algorithm is a public key encryption technique and is considered as the most secure way of encryption. It was invented by Rivest, Shamir and Adleman in year 1978 and hence name RSA algorithm.

Algorithm

The RSA algorithm holds the following features −

RSA algorithm is a popular exponentiation in a finite field over integers including prime numbers.
The integers used by this method are sufficiently large making it difficult to solve.
There are two sets of keys in this algorithm: private key and public key.

You will have to go through the following steps to work on RSA algorithm −

Step 1: Generate the RSA modulus

The initial procedure begins with selection of two prime numbers namely p and q, and then calculating their product N, as shown −

N=p*q

Here, let N be the specified large number.

Step 2: Derived Number (e)

Consider number e as a derived number which should be greater than 1 and less than (p-1) and (q-1). The primary condition will be that there should be no common factor of (p-1) and (q-1) except 1

Step 3: Public key

The specified pair of numbers n and e forms the RSA public key and it is made public.

Step 4: Private Key

Private Key d is calculated from the numbers p, q and e. The mathematical relationship between the numbers is as follows −

ed = 1 mod (p-1) (q-1)

The above formula is the basic formula for Extended Euclidean Algorithm, which takes p and q as the input parameters.

Encryption Formula

Consider a sender who sends the plain text message to someone whose public key is (n,e). To encrypt the plain text message in the given scenario, use the following syntax −

C = Pe mod n

Decryption Formula

The decryption process is very straightforward and includes analytics for calculation in a systematic approach. Considering receiver C has the private key d, the result modulus will be calculated as −

Plaintext = Cd mod n

Creating RSA Keys

In this chapter, we will focus on step wise implementation of RSA algorithm using Python.

Generating RSA keys

The following steps are involved in generating RSA keys −

Create two large prime numbers namely p and q. The product of these numbers will be called n, where n= p*q
Generate a random number which is relatively prime with (p-1) and (q-1). Let the number be called as e.
Calculate the modular inverse of e. The calculated inverse will be called as d.

Algorithms for generating RSA keys

We need two primary algorithms for generating RSA keys using Python − Cryptomath module and Rabin Miller module.

Cryptomath Module

The source code of cryptomath module which follows all the basic implementation of RSA algorithm is as follows −

def gcd(a, b):
   while a != 0:
      a, b = b % a, a
   return b

def findModInverse(a, m):
   if gcd(a, m) != 1:
      return None
   u1, u2, u3 = 1, 0, a
   v1, v2, v3 = 0, 1, m
   
   while v3 != 0:
      q = u3 // v3
         v1, v2, v3, u1, u2, u3 = (u1 - q * v1), (u2 - q * v2), (u3 - q * v3), v1, v2, v3
   return u1 % m

RabinMiller Module

The source code of RabinMiller module which follows all the basic implementation of RSA algorithm is as follows −

import random
def rabinMiller(num):
   s = num - 1
   t = 0
   
   while s % 2 == 0:
      s = s // 2
      t += 1
   for trials in range(5):
      a = random.randrange(2, num - 1)
      v = pow(a, s, num)
      if v != 1:
         i = 0
         while v != (num - 1):
            if i == t - 1:
               return False
            else:
               i = i + 1
               v = (v ** 2) % num
      return True
def isPrime(num):
   if (num 7< 2):
      return False
   lowPrimes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 
   67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 
   157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 
   251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313,317, 331, 337, 347, 349, 
   353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 
   457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 
   571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 
   673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 
   797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 
   911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997]
	
   if num in lowPrimes:
      return True
   for prime in lowPrimes:
      if (num % prime == 0):
         return False
   return rabinMiller(num)
def generateLargePrime(keysize = 1024):
   while True:
      num = random.randrange(2**(keysize-1), 2**(keysize))
      if isPrime(num):
         return num

The complete code for generating RSA keys is as follows −

import random, sys, os, rabinMiller, cryptomath

def main():
   makeKeyFiles('RSA_demo', 1024)

def generateKey(keySize):
   # Step 1: Create two prime numbers, p and q. Calculate n = p * q.
   print('Generating p prime...')
   p = rabinMiller.generateLargePrime(keySize)
   print('Generating q prime...')
   q = rabinMiller.generateLargePrime(keySize)
   n = p * q
	
   # Step 2: Create a number e that is relatively prime to (p-1)*(q-1).
   print('Generating e that is relatively prime to (p-1)*(q-1)...')
   while True:
      e = random.randrange(2 ** (keySize - 1), 2 ** (keySize))
      if cryptomath.gcd(e, (p - 1) * (q - 1)) == 1:
         break
   
   # Step 3: Calculate d, the mod inverse of e.
   print('Calculating d that is mod inverse of e...')
   d = cryptomath.findModInverse(e, (p - 1) * (q - 1))
   publicKey = (n, e)
   privateKey = (n, d)
   print('Public key:', publicKey)
   print('Private key:', privateKey)
   return (publicKey, privateKey)

def makeKeyFiles(name, keySize):
   # Creates two files 'x_pubkey.txt' and 'x_privkey.txt' 
      (where x is the value in name) with the the n,e and d,e integers written in them,
   # delimited by a comma.
   if os.path.exists('%s_pubkey.txt' % (name)) or os.path.exists('%s_privkey.txt' % (name)):
      sys.exit('WARNING: The file %s_pubkey.txt or %s_privkey.txt already exists! Use a different name or delete these files and re-run this program.' % (name, name))
   publicKey, privateKey = generateKey(keySize)
   print()
   print('The public key is a %s and a %s digit number.' % (len(str(publicKey[0])), len(str(publicKey[1])))) 
   print('Writing public key to file %s_pubkey.txt...' % (name))
   
   fo = open('%s_pubkey.txt' % (name), 'w')
	fo.write('%s,%s,%s' % (keySize, publicKey[0], publicKey[1]))
   fo.close()
   print()
   print('The private key is a %s and a %s digit number.' % (len(str(publicKey[0])), len(str(publicKey[1]))))
   print('Writing private key to file %s_privkey.txt...' % (name))
   
   fo = open('%s_privkey.txt' % (name), 'w')
   fo.write('%s,%s,%s' % (keySize, privateKey[0], privateKey[1]))
   fo.close()
# If makeRsaKeys.py is run (instead of imported as a module) call
# the main() function.
if __name__ == '__main__':
   main()

Output

The public key and private keys are generated and saved in the respective files as shown in the following output.

RSA Cipher Encryption

In this chapter, we will focus on different implementation of RSA cipher encryption and the functions involved for the same. You can refer or include this python file for implementing RSA cipher algorithm implementation.

The modules included for the encryption algorithm are as follows −

from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Signature import PKCS1_v1_5
from Crypto.Hash import SHA512, SHA384, SHA256, SHA, MD5
from Crypto import Random
from base64 import b64encode, b64decode
hash = "SHA-256"

We have initialized the hash value as SHA-256 for better security purpose. We will use a function to generate new keys or a pair of public and private key using the following code.

def newkeys(keysize):
   random_generator = Random.new().read
   key = RSA.generate(keysize, random_generator)
   private, public = key, key.publickey()
   return public, private
def importKey(externKey):
   return RSA.importKey(externKey)

For encryption, the following function is used which follows the RSA algorithm −

def encrypt(message, pub_key):
   cipher = PKCS1_OAEP.new(pub_key)
   return cipher.encrypt(message)

Two parameters are mandatory: message and pub_key which refers to Public key. A public key is used for encryption and private key is used for decryption.

The complete program for encryption procedure is mentioned below −

from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Signature import PKCS1_v1_5
from Crypto.Hash import SHA512, SHA384, SHA256, SHA, MD5
from Crypto import Random
from base64 import b64encode, b64decode
hash = "SHA-256"

def newkeys(keysize):
   random_generator = Random.new().read
   key = RSA.generate(keysize, random_generator)
   private, public = key, key.publickey()
   return public, private

def importKey(externKey):
   return RSA.importKey(externKey)

def getpublickey(priv_key):
   return priv_key.publickey()

def encrypt(message, pub_key):
   cipher = PKCS1_OAEP.new(pub_key)
   return cipher.encrypt(message)

RSA Cipher Decryption

This chapter is a continuation of the previous chapter where we followed step wise implementation of encryption using RSA algorithm and discusses in detail about it.

The function used to decrypt cipher text is as follows −

def decrypt(ciphertext, priv_key):
   cipher = PKCS1_OAEP.new(priv_key)
   return cipher.decrypt(ciphertext)

For public key cryptography or asymmetric key cryptography, it is important to maintain two important features namely Authentication and Authorization.

Authorization

Authorization is the process to confirm that the sender is the only one who have transmitted the message. The following code explains this −

def sign(message, priv_key, hashAlg="SHA-256"):
   global hash
   hash = hashAlg
   signer = PKCS1_v1_5.new(priv_key)
   
   if (hash == "SHA-512"):
      digest = SHA512.new()
   elif (hash == "SHA-384"):
      digest = SHA384.new()
   elif (hash == "SHA-256"):
      digest = SHA256.new()
   elif (hash == "SHA-1"):
      digest = SHA.new()
   else:
      digest = MD5.new()
   digest.update(message)
   return signer.sign(digest)

Authentication

Authentication is possible by verification method which is explained as below −

def verify(message, signature, pub_key):
   signer = PKCS1_v1_5.new(pub_key)
   if (hash == "SHA-512"):
      digest = SHA512.new()
   elif (hash == "SHA-384"):
      digest = SHA384.new()
   elif (hash == "SHA-256"):
      digest = SHA256.new()
   elif (hash == "SHA-1"):
      digest = SHA.new()
   else:
      digest = MD5.new()
   digest.update(message)
   return signer.verify(digest, signature)

The digital signature is verified along with the details of sender and recipient. This adds more weight age for security purposes.

RSA Cipher Decryption

You can use the following code for RSA cipher decryption −

from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Signature import PKCS1_v1_5
from Crypto.Hash import SHA512, SHA384, SHA256, SHA, MD5
from Crypto import Random
from base64 import b64encode, b64decode
hash = "SHA-256"

def newkeys(keysize):
   random_generator = Random.new().read
   key = RSA.generate(keysize, random_generator)
   private, public = key, key.publickey()
   return public, private

def importKey(externKey):
   return RSA.importKey(externKey)

def getpublickey(priv_key):
   return priv_key.publickey()

def encrypt(message, pub_key):
   cipher = PKCS1_OAEP.new(pub_key)
   return cipher.encrypt(message)

def decrypt(ciphertext, priv_key):
   cipher = PKCS1_OAEP.new(priv_key)
   return cipher.decrypt(ciphertext)

def sign(message, priv_key, hashAlg = "SHA-256"):
   global hash
   hash = hashAlg
   signer = PKCS1_v1_5.new(priv_key)
   
   if (hash == "SHA-512"):
      digest = SHA512.new()
   elif (hash == "SHA-384"):
      digest = SHA384.new()
   elif (hash == "SHA-256"):
      digest = SHA256.new()
   elif (hash == "SHA-1"):
      digest = SHA.new()
   else:
      digest = MD5.new()
   digest.update(message)
   return signer.sign(digest)

def verify(message, signature, pub_key):
   signer = PKCS1_v1_5.new(pub_key)
   if (hash == "SHA-512"):
      digest = SHA512.new()
   elif (hash == "SHA-384"):
      digest = SHA384.new()
   elif (hash == "SHA-256"):
      digest = SHA256.new()
   elif (hash == "SHA-1"):
      digest = SHA.new()
   else:
      digest = MD5.new()
   digest.update(message)
   return signer.verify(digest, signature)

Hacking RSA Cipher

Hacking RSA cipher is possible with small prime numbers, but it is considered impossible if it is used with large numbers. The reasons which specify why it is difficult to hack RSA cipher are as follows −

Brute force attack would not work as there are too many possible keys to work through. Also, this consumes a lot of time.
Dictionary attack will not work in RSA algorithm as the keys are numeric and does not include any characters in it.
Frequency analysis of the characters is very difficult to follow as a single encrypted block represents various characters.
There are no specific mathematical tricks to hack RSA cipher.

The RSA decryption equation is −

M = C^d mod n

With the help of small prime numbers, we can try hacking RSA cipher and the sample code for the same is mentioned below −

def p_and_q(n):
   data = []
   for i in range(2, n):
      if n % i == 0:
         data.append(i)
   return tuple(data)

def euler(p, q):
   return (p - 1) * (q - 1)

def private_index(e, euler_v):
   for i in range(2, euler_v):
      if i * e % euler_v == 1:
         return i

def decipher(d, n, c):
   return c ** d % n
	def main():
      e = int(input("input e: "))
      n = int(input("input n: "))
      c = int(input("input c: "))
      
      # t = 123
      # private key = (103, 143)
      p_and_q_v = p_and_q(n)
      # print("[p_and_q]: ", p_and_q_v)
      euler_v = euler(p_and_q_v[0], p_and_q_v[1])
      
      # print("[euler]: ", euler_v)
      d = private_index(e, euler_v)
      plain = decipher(d, n, c)
      print("plain: ", plain)
if __name__ == "__main__":
   main()

Output

The above code produces the following output −

Previous Page Print Page