Viewing & Clipping

The primary use of clipping in computer graphics is to remove objects, lines, or line segments that are outside the viewing pane. The viewing transformation is insensitive to the position of points relative to the viewing volume − especially those points behind the viewer − and it is necessary to remove these points before generating the view.

Point Clipping

Clipping a point from a given window is very easy. Consider the following figure, where the rectangle indicates the window. Point clipping tells us whether the given point (X, Y) is within the given window or not; and decides whether we will use the minimum and maximum coordinates of the window.

The X-coordinate of the given point is inside the window, if X lies in between Wx1 ≤ X ≤ Wx2. Same way, Y coordinate of the given point is inside the window, if Y lies in between Wy1 ≤ Y ≤ Wy2.

Line Clipping

The concept of line clipping is same as point clipping. In line clipping, we will cut the portion of line which is outside of window and keep only the portion that is inside the window.

Cohen-Sutherland Line Clippings

This algorithm uses the clipping window as shown in the following figure. The minimum coordinate for the clipping region is $(XW_{min,} YW_{min})$ and the maximum coordinate for the clipping region is $(XW_{max,} YW_{max})$.

We will use 4-bits to divide the entire region. These 4 bits represent the Top, Bottom, Right, and Left of the region as shown in the following figure. Here, the TOP and LEFT bit is set to 1 because it is the TOP-LEFT corner.

There are 3 possibilities for the line −

• Line can be completely inside the window (This line should be accepted).

• Line can be completely outside of the window (This line will be completely removed from the region).

• Line can be partially inside the window (We will find intersection point and draw only that portion of line that is inside region).

Algorithm

Step 1 − Assign a region code for each endpoints.

Step 2 − If both endpoints have a region code 0000 then accept this line.

Step 3 − Else, perform the logical ANDoperation for both region codes.

Step 3.1 − If the result is not 0000, then reject the line.

Step 3.2 − Else you need clipping.

Step 3.2.1 − Choose an endpoint of the line that is outside the window.

Step 3.2.2 − Find the intersection point at the window boundary (base on region code).

Step 3.2.3 − Replace endpoint with the intersection point and update the region code.

Step 3.2.4 − Repeat step 2 until we find a clipped line either trivially accepted or trivially rejected.

Step 4 − Repeat step 1 for other lines.

Cyrus-Beck Line Clipping Algorithm

This algorithm is more efficient than Cohen-Sutherland algorithm. It employs parametric line representation and simple dot products.

Parametric equation of line is −

P0P1:P(t) = P0 + t(P1 - P0)

Let N_i be the outward normal edge E_i. Now pick any arbitrary point P_Ei on edge E_i then the dot product N_i.[P(t) – P_Ei] determines whether the point P(t) is “inside the clip edge” or “outside” the clip edge or “on” the clip edge.

The point P(t) is inside if N_i.[P(t) – P_Ei] < 0

The point P(t) is outside if N_i.[P(t) – P_Ei] > 0

The point P(t) is on the edge if N_i.[P(t) – P_Ei] = 0 (Intersection point)

N_i.[P(t) – P_Ei] = 0

N_i.[ P₀ + t(P₁ - P₀) – P_Ei] = 0 (Replacing P(t) with P₀ + t(P₁ - P₀))

N_i.[P₀ – P_Ei] + N_i.t[P₁ - P₀] = 0

N_i.[P₀ – P_Ei] + N_i∙tD = 0 (substituting D for [P₁ - P₀])

N_i.[P₀ – P_Ei] = - N_i∙tD

The equation for t becomes,

$$t = \tfrac{N_{i}.[P_{o} - P_{Ei}]}{{- N_{i}.D}}$$

It is valid for the following conditions −

• N_i ≠ 0 (error cannot happen)
• D ≠ 0 (P₁ ≠ P₀)
• N_i∙D ≠ 0 (P₀P₁ not parallel to E_i)

Polygon Clipping (Sutherland Hodgman Algorithm)

A polygon can also be clipped by specifying the clipping window. Sutherland Hodgeman polygon clipping algorithm is used for polygon clipping. In this algorithm, all the vertices of the polygon are clipped against each edge of the clipping window.

First the polygon is clipped against the left edge of the polygon window to get new vertices of the polygon. These new vertices are used to clip the polygon against right edge, top edge, bottom edge, of the clipping window as shown in the following figure.

While processing an edge of a polygon with clipping window, an intersection point is found if edge is not completely inside clipping window and the a partial edge from the intersection point to the outside edge is clipped. The following figures show left, right, top and bottom edge clippings −

Text Clipping

Various techniques are used to provide text clipping in a computer graphics. It depends on the methods used to generate characters and the requirements of a particular application. There are three methods for text clipping which are listed below −

• All or none string clipping
• All or none character clipping
• Text clipping

The following figure shows all or none string clipping −

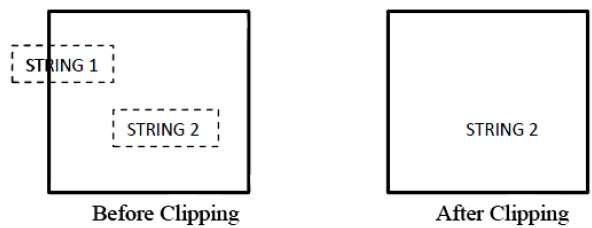
In all or none string clipping method, either we keep the entire string or we reject entire string based on the clipping window. As shown in the above figure, STRING2 is entirely inside the clipping window so we keep it and STRING1 being only partially inside the window, we reject.

The following figure shows all or none character clipping −

This clipping method is based on characters rather than entire string. In this method if the string is entirely inside the clipping window, then we keep it. If it is partially outside the window, then −

• You reject only the portion of the string being outside

• If the character is on the boundary of the clipping window, then we discard that entire character and keep the rest string.

The following figure shows text clipping −

This clipping method is based on characters rather than the entire string. In this method if the string is entirely inside the clipping window, then we keep it. If it is partially outside the window, then

• You reject only the portion of string being outside.

• If the character is on the boundary of the clipping window, then we discard only that portion of character that is outside of the clipping window.

Bitmap Graphics

A bitmap is a collection of pixels that describes an image. It is a type of computer graphics that the computer uses to store and display pictures. In this type of graphics, images are stored bit by bit and hence it is named Bit-map graphics. For better understanding let us consider the following example where we draw a smiley face using bit-map graphics.

Now we will see how this smiley face is stored bit by bit in computer graphics.

By observing the original smiley face closely, we can see that there are two blue lines which are represented as B1, B2 and E1, E2 in the above figure.

In the same way, the smiley is represented using the combination bits of A4, B5, C6, D6, E5, and F4 respectively.

The main disadvantages of bitmap graphics are −

• We cannot resize the bitmap image. If you try to resize, the pixels get blurred.

• Colored bitmaps can be very large.