Artificial Neural Network - Genetic Algorithm
Nature has always been a great source of inspiration to all mankind. Genetic Algorithms (GAs) are search-based algorithms based on the concepts of natural selection and genetics. GAs are a subset of a much larger branch of computation known as Evolutionary Computation.
GAs was developed by John Holland and his students and colleagues at the University of Michigan, most notably David E. Goldberg and has since been tried on various optimization problems with a high degree of success.
In GAs, we have a pool or a population of possible solutions to the given problem. These solutions then undergo recombination and mutation (like in natural genetics), producing new children, and the process is repeated over various generations. Each individual (or candidate solution) is assigned a fitness value (based on its objective function value) and the fitter individuals are given a higher chance to mate and yield more “fitter” individuals. This is in line with the Darwinian Theory of “Survival of the Fittest”.
In this way, we keep “evolving” better individuals or solutions over generations, till we reach a stopping criterion.
Genetic Algorithms are sufficiently randomized in nature, however they perform much better than random local search (in which we just try various random solutions, keeping track of the best so far), as they exploit historical information as well.
Advantages of GAs
GAs have various advantages which have made them immensely popular. These include −
Does not require any derivative information (which may not be available for many real-world problems).
Is faster and more efficient as compared to the traditional methods.
Has very good parallel capabilities.
Optimizes both continuous and discrete functions as well as multi-objective problems.
Provides a list of “good” solutions and not just a single solution.
Always gets an answer to the problem, which gets better over the time.
Useful when the search space is very large and there are large number of parameters involved.
Limitations of GAs
Like any technique, GAs also suffers from a few limitations. These include −
GAs are not suited for all problems, especially problems which are simple and for which derivative information is available.
Fitness value is calculated repeatedly, which might be computationally expensive for some problems.
Being stochastic, there are no guarantees on the optimality or the quality of the solution.
If not implemented properly, GA may not converge to the optimal solution.
GA – Motivation
Genetic Algorithms have the ability to deliver a “good-enough” solution “fast-enough”. This makes Gas attractive for use in solving optimization problems. The reasons why GAs are needed are as follows −
Solving Difficult Problems
In computer science, there is a large set of problems, which are NP-Hard. What this essentially means is that, even the most powerful computing systems take a very long time (even years!) to solve that problem. In such a scenario, GAs prove to be an efficient tool to provide usable near-optimal solutions in a short amount of time.
Failure of Gradient Based Methods
Traditional calculus based methods work by starting at a random point and by moving in the direction of the gradient, till we reach the top of the hill. This technique is efficient and works very well for single-peaked objective functions like the cost function in linear regression. However, in most real-world situations, we have a very complex problem called as landscapes, made of many peaks and many valleys, which causes such methods to fail, as they suffer from an inherent tendency of getting stuck at the local optima as shown in the following figure.
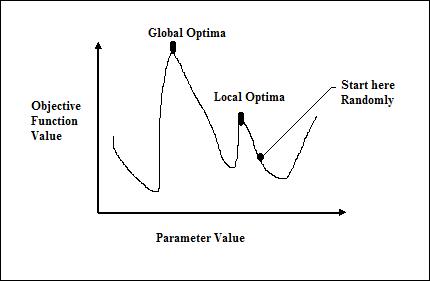
Getting a Good Solution Fast
Some difficult problems like the Travelling Salesman Problem (TSP), have real-world applications like path finding and VLSI Design. Now imagine that you are using your GPS Navigation system, and it takes a few minutes (or even a few hours) to compute the “optimal” path from the source to destination. Delay in such real-world applications is not acceptable and therefore a “good-enough” solution, which is delivered “fast” is what is required.
How to Use GA for Optimization Problems?
We already know that optimization is an action of making something such as design, situation, resource, and system as effective as possible. Optimization process is shown in the following diagram.

Stages of GA Mechanism for Optimization Process
Followings are the stages of GA mechanism when used for optimization of problems.
Generate the initial population randomly.
Select the initial solution with the best fitness values.
Recombine the selected solutions using mutation and crossover operators.
Insert offspring into the population.
Now if the stop condition is met, then return the solution with their best fitness value. Else, go to step 2.




