Analog Communication - DSBSC Modulation

In the process of Amplitude Modulation, the modulated wave consists of the carrier wave and two sidebands. The modulated wave has the information only in the sidebands. Sideband is nothing but a band of frequencies, containing power, which are the lower and higher frequencies of the carrier frequency.

The transmission of a signal, which contains a carrier along with two sidebands can be termed as Double Sideband Full Carrier system or simply DSBFC. It is plotted as shown in the following figure.

However, such a transmission is inefficient. Because, two-thirds of the power is being wasted in the carrier, which carries no information.

If this carrier is suppressed and the saved power is distributed to the two sidebands, then such a process is called as Double Sideband Suppressed Carrier system or simply DSBSC. It is plotted as shown in the following figure.

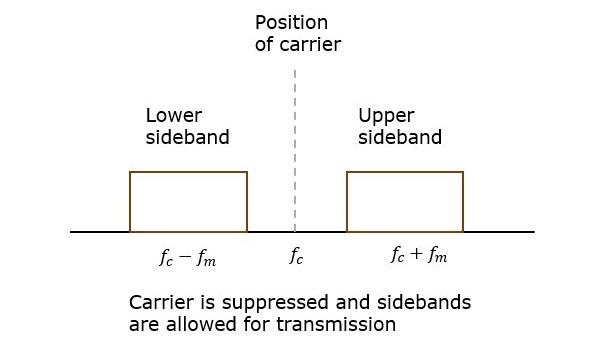
Mathematical Expressions

Let us consider the same mathematical expressions for modulating and carrier signals as we have considered in the earlier chapters.

i.e., Modulating signal

$$m\left ( t \right )=A_m \cos \left ( 2 \pi f_mt\right )$$

Carrier signal

$$c\left ( t \right )=A_c \cos \left ( 2 \pi f_ct\right )$$

Mathematically, we can represent the equation of DSBSC wave as the product of modulating and carrier signals.

$$s\left ( t \right )=m\left ( t \right )c\left ( t \right )$$

$$\Rightarrow s\left ( t \right )=A_mA_c \cos \left ( 2 \pi f_mt \right )\cos \left ( 2 \pi f_ct \right )$$

Bandwidth of DSBSC Wave

We know the formula for bandwidth (BW) is

$$BW=f_{max}-f_{min}$$

Consider the equation of DSBSC modulated wave.

$$s\left ( t \right )=A_mA_c \cos\left ( 2 \pi f_mt \right ) \cos(2 \pi f_ct)$$

$$\Rightarrow s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c+f_m \right ) t\right ]+\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c-f_m \right ) t\right ]$$

The DSBSC modulated wave has only two frequencies. So, the maximum and minimum frequencies are $f_c+f_m$ and $f_c-f_m$ respectively.

i.e.,

$f_{max}=f_c+f_m$ and $f_{min}=f_c-f_m$

Substitute, $f_{max}$ and $f_{min}$ values in the bandwidth formula.

$$BW=f_c+f_m-\left ( f_c-f_m \right )$$

$$\Rightarrow BW=2f_m$$

Thus, the bandwidth of DSBSC wave is same as that of AM wave and it is equal to twice the frequency of the modulating signal.

Power Calculations of DSBSC Wave

Consider the following equation of DSBSC modulated wave.

$$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi \left ( f_c+f_m \right ) t\right ]+\frac{A_mA_c}{2} \cos\left [ 2 \pi \left ( f_c-f_m \right ) t\right ]$$

Power of DSBSC wave is equal to the sum of powers of upper sideband and lower sideband frequency components.

$$P_t=P_{USB}+P_{LSB}$$

We know the standard formula for power of cos signal is

$$P=\frac{{v_{rms}}^{2}}{R}=\frac{\left ( v_m\sqrt{2}\right )^2}{R}$$

First, let us find the powers of upper sideband and lower sideband one by one.

Upper sideband power

$$P_{USB}=\frac{\left ( A_mA_c / 2\sqrt{2}\right )^2}{R}=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}$$

Similarly, we will get the lower sideband power same as that of upper sideband power.

$$P_{USB}=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}$$

Now, let us add these two sideband powers in order to get the power of DSBSC wave.

$$P_t=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}+\frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}$$

$$\Rightarrow P_t=\frac{{A_{m}}^{2}{A_{c}}^{2}}{4R}$$

Therefore, the power required for transmitting DSBSC wave is equal to the power of both the sidebands.